题目内容
(8分)
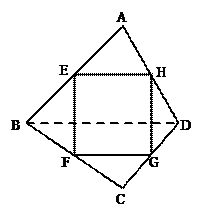
已知四边形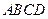 是空间四边形,
是空间四边形,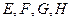 分别是边
分别是边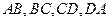 的中点,求证:四边形
的中点,求证:四边形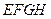 是平行四边形。
是平行四边形。
已知四边形
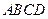 是空间四边形,
是空间四边形,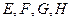 分别是边
分别是边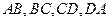 的中点,求证:四边形
的中点,求证:四边形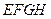 是平行四边形。
是平行四边形。
证明 由题意知EH 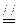 BD FG
BD FG 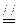 BD ∴EH
BD ∴EH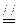 FG
FG
∴四边形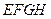 是平行四边形
是平行四边形
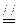 BD FG
BD FG 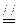 BD ∴EH
BD ∴EH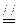 FG
FG∴四边形
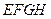 是平行四边形
是平行四边形略

练习册系列答案
相关题目
题目内容
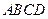 是空间四边形,
是空间四边形,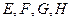 分别是边
分别是边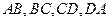 的中点,求证:四边形
的中点,求证:四边形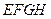 是平行四边形。
是平行四边形。
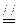 BD FG
BD FG 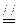 BD ∴EH
BD ∴EH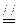 FG
FG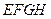 是平行四边形
是平行四边形