题目内容
(本小题满分12分)
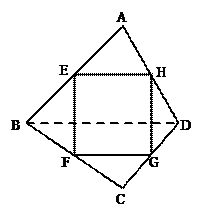
如图,四棱锥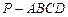 的底面
的底面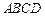 为菱形,
为菱形,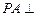 平面
平面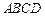 ,
,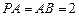 ,
,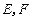 分别为
分别为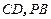 的中点,
的中点,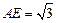 .
.

(Ⅰ)求证: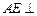 平面
平面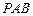 .
.
(Ⅱ)求三棱锥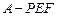 的体积.
的体积.
如图,四棱锥
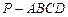 的底面
的底面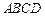 为菱形,
为菱形,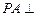 平面
平面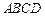 ,
,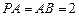 ,
,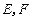 分别为
分别为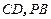 的中点,
的中点,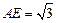 .
.
(Ⅰ)求证:
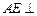 平面
平面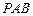 .
.(Ⅱ)求三棱锥
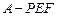 的体积.
的体积.19.(Ⅰ)证明:∵四边形
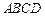 是菱形,
是菱形,∴
 .…………………1分
.…………………1分在
 中,
中,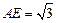 ,
, ,
,∴
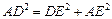 .
.∴
 ,即
,即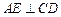 .
.又
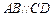 , ∴
, ∴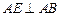 .…………………2分
.…………………2分∵
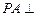 平面
平面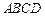 ,
, 平面
平面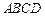 ,
,∴
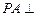
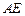 .又∵
.又∵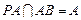 ,
,∴
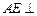 平面
平面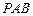 ,………………………………………4分
,………………………………………4分又∵
 平面
平面 ,
,平面
 平面
平面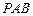 . ………………………………6分
. ………………………………6分又
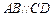 , ∴
, ∴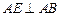 .
.∵
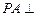 平面
平面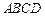 ,
, 平面
平面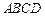 ,
,∴
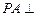
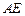 . ………………………………………5分
. ………………………………………5分又∵
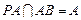 ,
,∴
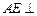 平面
平面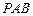 . ……………………………6分
. ……………………………6分(Ⅱ)解法一:由(Ⅰ)知,
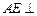 平面
平面
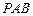 ,
,所以,
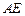 是三棱锥
是三棱锥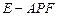 底面上的高,且
底面上的高,且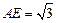 . …………7分
. …………7分∵
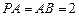
∴
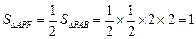 ,…………………10分
,…………………10分∴
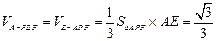 ,………………11分
,………………11分所以,三棱锥
 的体积为
的体积为 . ………………12分
. ………………12分解法二:
 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 柱
柱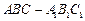 中,已知
中,已知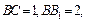
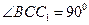 ,
,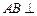 侧面
侧面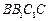
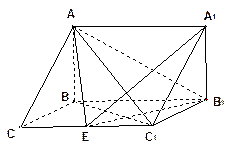
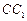 (不包含端点
(不包含端点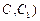 上确定一点
上确定一点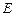 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).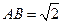 ,求二面角
,求二面角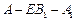 的大小.
的大小.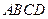 是
是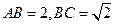 的矩形,
的矩形,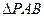 是正三角形,将
是正三角形,将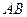 折起,使
折起,使 如图2,
如图2,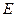 为
为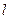 过点
过点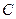 且垂直于矩形
且垂直于矩形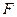 是直线
是直线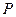 位于平面
位于平面
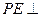 平面
平面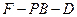 的平面角为
的平面角为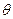 ,若
,若 ,求线段
,求线段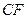 长的取值范围。
长的取值范围。 角板按图甲方式拼好,其中
角板按图甲方式拼好,其中 ,
,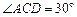 ,
,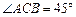 ,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
 :O为线段AB中点;
:O为线段AB中点;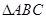 的三个顶点均在球O的球面上,且AB=AC=1,
的三个顶点均在球O的球面上,且AB=AC=1,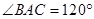 ,直线OA与平面ABC所成的角的正弦值为
,直线OA与平面ABC所成的角的正弦值为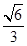 ,则球面上B、C两点间的球面距离为 。
,则球面上B、C两点间的球面距离为 。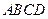 是空间四边形,
是空间四边形,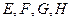 分别是边
分别是边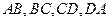 的中点,求证:四边形
的中点,求证:四边形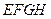 是平行四边形。
是平行四边形。