题目内容
17.解方程:3x4+5x3-17x2-13x+6=0.分析 通过因式分解即可解出.
解答 解:∵3x4+5x3-17x2-13x+6=(3x4+5x3+2x2)-(19x2+13x-6)=x2(3x+2)(x+1)-(19x-6)(x+1)
=(x+1)(3x3+2x2-19x+6)
又3x3+2x2-19x+6=3(x3-8)+2x2-19x+30=3(x-2)(x2+2x+4)+(2x-15)(x-2)=(x-2)(3x2+8x-3)=(x-2)(3x-1)(x+3).
∴原方程化为:(x+1)(x-2)(3x-1)(x+3)=0,
解得x=-3,-1,$\frac{1}{3}$,2.
∴原方程的实数根为x=-3,-1,$\frac{1}{3}$,2.
点评 本题考查了通过因式分解解方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.圆锥的母线长为l,高为$\frac{1}{2}$l,则过圆锥顶点的最大截面的面积为( )
| A. | $\frac{\sqrt{3}}{4}$l2 | B. | $\frac{1}{2}$l2 | C. | $\frac{\sqrt{3}}{2}$l2 | D. | $\frac{1}{4}$l2 |
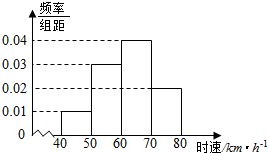 200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.
200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在(50,60)的汽车大约有60辆.