Question

【题目】如下图所示，在三棱锥P－ABC中，PA⊥底面ABC，PA＝AB，∠ABC＝60°，∠BCA＝90°，点D，E分别在棱PB，PC上，且DE∥BC.

(1)求证：BC⊥平面PAC；

(2)当D为PB的中点时，求AD与平面PAC所成的角的正弦值；

(3)是否存在点E，使得二面角A－DE－P为直二面角？并说明理由．

Answer 1

【答案】（1）见证明；（2） (3)见解析

【解析】

建立如图所示的空间直角坐标系，（1）通过证明，再结合即可得结论；（2）结合（1）中的结论进一步说明是与平面所成的角，先通过向量夹角公式求出余弦值，再求正弦值；（3）由已知条件推导出为二面角的平面角，由此能推导出存在点使得二面角是直二面角．

以A为原点，，分别为y轴、z轴的正方向，

过A点且垂直于平面PAB的直线为x轴，建立空间直角坐标系，

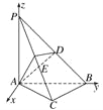
设PA＝a，由已知可得：A(0,0,0)，B(0，a，0)，C，P(0,0，a)．

(1)＝(0,0，a)，＝，∴＝0，∴⊥，∴BC⊥AP，

又∵∠BCA＝90°，∴BC⊥AC，∴BC⊥平面PAC.

(2)∵D为PB的中点，DE∥BC，∴E为PC的中点，

∴D，E，

∴由(1)知，BC⊥平面PAC，∴DE⊥平面PAC，垂足为点E，

∴∠DAE是AD与平面PAC所成的角，

∵＝，＝，∴cos∠DAE＝＝，

∴AD与平面PAC所成的角的正弦值为.

(3)∵DE∥BC，又由(1)知BC⊥平面PAC，∴DE⊥平面PAC，

又∵AE平面PAC，PE平面PAC，

∴DE⊥AE，DE⊥PE，∴∠AEP为二面角A－DE－P的平面角．

∵PA⊥底面ABC，∴PA⊥AC，∴∠PAC＝90°，

∴在棱PC上存在一点E，使得AE⊥PC，这时∠AEP＝90°，

故存在点E，使得二面角A－DE－P是直二面角．