题目内容
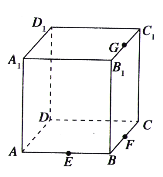
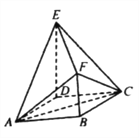
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]()
![]() .
.
(1)当![]() 长为多少时,平面
长为多少时,平面![]() 平面
平面![]() ?
?
(2)在(1)的条件下,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)二面角E-AC-F的余弦值为![]() .
.
【解析】试题分析:(1)先根据条件建立空间直角坐标系,设立各点坐标,利用向量垂直列方程组,解得各面法向量,根据平面垂直得两法向量数量积为零,解得![]() 长,(2)利用方程组先解出各面法向量,根据向量数量积求两法向量夹角,再根据二面角与向量夹角关系求结果.
长,(2)利用方程组先解出各面法向量,根据向量数量积求两法向量夹角,再根据二面角与向量夹角关系求结果.
试题解析:(1)连接BD交AC于点O,则AC⊥BD.
取EF的中点G,连接OG,则OG∥DE.
∵DE⊥平面ABCD,∴OG⊥平面ABCD.
∴OG,AC,BD两两垂直.
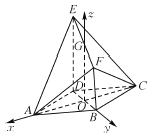
∴以AC,BD,OG所在直线分别作为x轴,y轴,z轴建立空间直角坐标系(如图),
 设
设![]() ,
,
由题意,易求![]() ,
,
![]()
∴![]() ,
,
![]()
设平面AEF,平面CEF的法向量分别为![]() ,
,![]()
由![]() ,
,![]() ,得
,得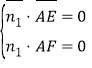 ,∴
,∴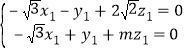
解得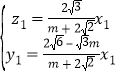 . 令
. 令![]() ,∴
,∴![]() .
.
同理可求![]() .
.
若平面AEF⊥平面CEF,则![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
即BF长为![]() 时,平面AEF⊥平面CEF.
时,平面AEF⊥平面CEF.
(2)当![]() 时,
时,![]() ,
,
![]()
∴![]() ,
,![]() ,∴EF⊥AF,EF⊥CF,
,∴EF⊥AF,EF⊥CF,
∴EF⊥平面AFC,
∴平面AFC的一个法向量为![]() ,
,
设平面AEC的一个法向量为![]() ,则
,则
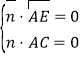 ,∴
,∴![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() .
.
从而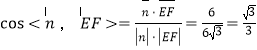 .
.
故所求的二面角E-AC-F的余弦值为![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】某地公共电汽车和地铁按照里程分段计价,具体如下表:
乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
乘坐地铁方案 | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含) |
已知在一号线地铁上,任意一站到![]() 站的票价不超过5元,现从那些只乘坐一号线地铁,且在
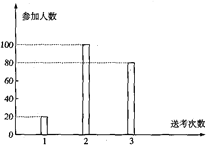
站的票价不超过5元,现从那些只乘坐一号线地铁,且在![]() 站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
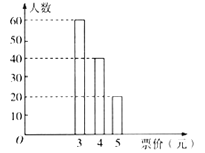
(Ⅰ)如果从那些只乘坐一号线地铁,且在![]() 站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6名学生中票价为3、4、5元的人数分别为3,2,1人,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐一号线地铁从![]() 地到
地到![]() 站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为
站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为![]() 公里,试写出
公里,试写出![]() 的取值范围.
的取值范围.
【题目】在一次诗词知识竞赛调查中,发现参赛选手分为两个年龄(单位:岁)段:![]() ,
,![]() ,其中答对诗词名句与否的人数如图所示.
,其中答对诗词名句与否的人数如图所示.
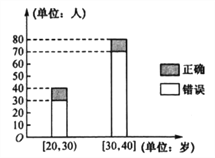
(1)完成下面2×2列联表;
年龄段 | 正确 | 错误 | 合计 |
| |||
| |||
合计 |
(2)是否有90%的把握认为答对诗词名句与年龄有关,请说明你的理由;
(3)现按年龄段分层抽样选取6名选手,若从这6名选手中选取3名选手,求3名选手中年龄在![]() 岁范围人数的分布列和数学期望.
岁范围人数的分布列和数学期望.