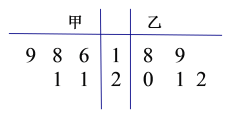
题目内容
【题目】已知函数f(x)=2x-![]() .
.
(1)判断函数的奇偶性,并证明;
(2)用单调性的定义证明函数f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
【答案】(1)函数f(x)=2x-![]() 是奇函数.
是奇函数.
证明如下:易知f(x)的定义域为{x|x≠0},关于原点对称.
因为f(-x)=2(-x)-![]() =-2x+
=-2x+![]() =-
=-![]() =-f(x),所以f(x)是奇函数.
=-f(x),所以f(x)是奇函数.
(2)证明:任取x1,x2∈(0,+∞),且x1<x2,
则f(x2)-f(x1)=2x2-![]() -
-![]() =2(x2-x1)+5
=2(x2-x1)+5![]() =(x2-x1)
=(x2-x1)![]() ,
,
因为0<x1<x2,所以x2-x1>0,x1x2>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
【解析】
(1)由定义判断![]() 与
与![]() 的关系,即可判断函数奇偶性;
的关系,即可判断函数奇偶性;
(2)由定义证明单调性,假设定义域内的两自变量的值![]() ,作差求
,作差求![]() 的符号,进而判断单调性.
的符号,进而判断单调性.
(1)函数f(x)=2x-![]() 是奇函数.
是奇函数.
证明如下:易知f(x)的定义域为{x|x≠0},关于原点对称.
因为f(-x)=2(-x)-![]() =-2x+
=-2x+![]() =-
=-![]() =-f(x),所以f(x)是奇函数.
=-f(x),所以f(x)是奇函数.
(2)证明:任取x1,x2∈(0,+∞),且x1<x2,
则f(x2)-f(x1)
=2x2-![]() -
-![]()
=2(x2-x1)+5![]()
=(x2-x1)![]() ,
,
因为0<x1<x2,所以x2-x1>0,x1x2>0,
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)=2x-![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目