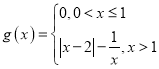Question

【题目】已知抛物线的顶点为平面直角坐标系的坐标原点，焦点为圆的圆心.经过点的直线交抛物线于两点，交圆于两点，在第一象限，在第四象限.

（1）求抛物线的方程；

（2）是否存在直线使是与的等差中项？若存在，求直线的方程；若不存在，请说明理由.

Answer 1

【答案】（1）抛物线E的方程为；（2）存在满足要求的直线或直线.

【解析】试题分析：（1）先根据圆的标准方程得圆心，再根据抛物线性质得p，即得抛物线的方程；（2）由题意得，再根据条件得.设直线方程，并与抛物线方程联立，利用韦达定理以及弦长公式求，解出斜率k.

试题解析：（1）∵圆F的方程为，

∴圆心F的坐标为（2，0），半径r=1.

根据题意设抛物线E的方程为，

∴，解得p=4.

∴抛物线E的方程为.

（2） ∵是与的等差中项，

∴.

∴.

讨论：

若垂直于x轴，则的方程为x=2，代入，解得.

此时|AD|=8，不满足题意；

若不垂直于x轴，则设的斜率为k（k≠0），此时的方程为，

由，得.

设，则.

∵拋物线E的准线方程为x=-2，

∴

∴，解得.

当时，化为.

∵，∴有两个不相等实数根.

∴满足题意.

∴存在满足要求的直线或直线.