题目内容
2.求直线l1:2x-y-2=0关于直线L:x-y-1=0对称的直线l2的方程为x-2y-1=0.分析 设直线l2上任意一点为P(x,y),则P关于直线L:x-y-1=0的对称点P′(m,n)在直线l1上,由对称性可得mn的方程组,解方程组代入直线l1化简得到的xy的方程即为所求.
解答 解:设直线l2上任意一点为P(x,y),
则P关于直线L:x-y-1=0的对称点P′(m,n)在直线l1上,
由对称性可得$\left\{\begin{array}{l}{\frac{y-n}{x-m}•1=-1}\\{\frac{x+m}{2}-\frac{y+n}{2}-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=y+1}\\{n=x-1}\end{array}\right.$,
代入直线l1可得2(y+1)-(x-1)-2=0,
化简可得所求直线方程为:x-2y-1=0
故答案为:x-2y-1=0
点评 本题考查直线的对称性,涉及直线垂直和中点公式,属基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
12.函数f(x)=loga(2-ax2)在(0,1)上为减函数,则实数a的取值范围是( )
| A. | [$\frac{1}{2}$,1) | B. | (1,2) | C. | (1,2] | D. | ($\frac{1}{2}$,1) |
13.函数y=log2(x2+2x-3)的单调递减区间为( )
| A. | (-∞,-3) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-3,-1) |
11.已知sin(π-α)=-$\frac{\sqrt{10}}{10}$,则$\frac{2si{n}^{2}α+sin2α}{cos(α-\frac{π}{4})}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{2\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
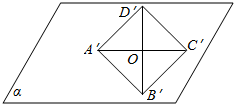 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.