题目内容
17．求函数f（x）=x+$\frac{1}{2x-4}$在（2，+∞）上的最低点坐标．分析 通过基本不等式求解函数的最值，推出结果即可．
解答 解：x∈（2，+∞），x-2＞0，
函数f（x）=x+$\frac{1}{2x-4}$=x-2+$\frac{1}{2x-4}$+2≥2$\sqrt{（x-2）×\frac{1}{2x-4}}$+2=2+$\sqrt{2}$，
当且仅当x-2=$\frac{1}{2x-4}$，即x=2+$\frac{\sqrt{2}}{2}$时取等号，
此时f（x）=$2+\frac{\sqrt{2}}{2}+\frac{1}{2（2+\frac{\sqrt{2}}{2}）-4}$=2+$\sqrt{2}$．
函数f（x）=x+$\frac{1}{2x-4}$在（2，+∞）上的最低点坐标（2+$\frac{\sqrt{2}}{2}$，$2+\sqrt{2}$）．
点评 本题考查基本不等式在最值中的应用，考查计算能力．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
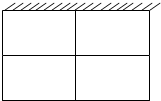如图所示，某畜牧基地要围成相同面积的羊圈4间，一面可利用原有的墙壁，其余各面用篱笆围成，篱笆总长为36m，则每间羊圈的长和宽各为多少时，羊圈面积最大？