题目内容
如图所示,在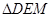 中,
中,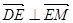 ,
,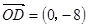 ,N在y轴上,且
,N在y轴上,且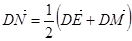 ,点E在x轴上移动.
,点E在x轴上移动.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)过点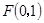 作互相垂直的两条直线
作互相垂直的两条直线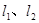 ,
,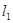 与点M的轨迹交于点A、B,
与点M的轨迹交于点A、B,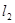 与点M的轨迹交于点C、D,求
与点M的轨迹交于点C、D,求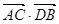 的最小值.
的最小值.
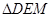 中,
中,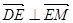 ,
,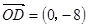 ,N在y轴上,且
,N在y轴上,且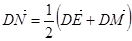 ,点E在x轴上移动.
,点E在x轴上移动.(Ⅰ)求点M的轨迹方程;
(Ⅱ)过点
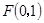 作互相垂直的两条直线
作互相垂直的两条直线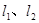 ,
,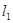 与点M的轨迹交于点A、B,
与点M的轨迹交于点A、B,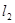 与点M的轨迹交于点C、D,求
与点M的轨迹交于点C、D,求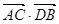 的最小值.
的最小值.(Ⅰ)设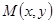 ,
,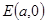 ,则
,则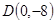 ,
,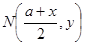
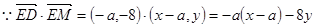 且
且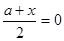 ,即
,即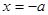
∴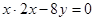 , 所以点F的轨迹方程为
, 所以点F的轨迹方程为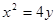 .(
.(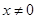 ) (6分)
) (6分)
(Ⅱ)设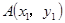 ,
,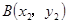 ,
,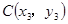 ,
,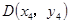 ,
,
直线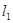 的方程为:
的方程为: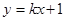 ,
,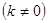 ,则直线
,则直线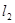 的方程为
的方程为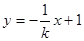
由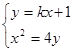 得:
得: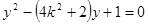 ;
;
则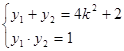 同理可得:
同理可得: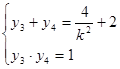
∵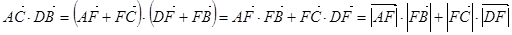
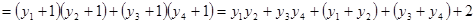
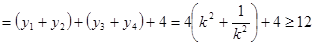 ,当且仅当
,当且仅当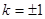 时,取等号.
时,取等号.
∴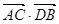 的最小值为12.
的最小值为12.
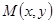 ,
,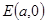 ,则
,则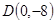 ,
,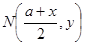
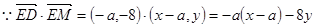 且
且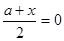 ,即
,即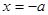
∴
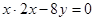 , 所以点F的轨迹方程为
, 所以点F的轨迹方程为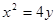 .(
.(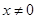 ) (6分)
) (6分)(Ⅱ)设
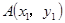 ,
,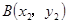 ,
,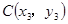 ,
,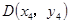 ,
,直线
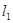 的方程为:
的方程为: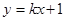 ,
,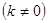 ,则直线
,则直线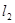 的方程为
的方程为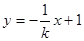
由
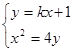 得:
得: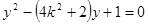 ;
;则
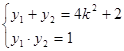 同理可得:
同理可得: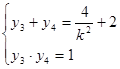
∵
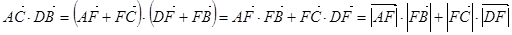
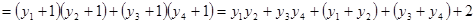
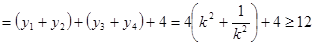 ,当且仅当
,当且仅当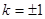 时,取等号.
时,取等号.∴
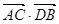 的最小值为12.
的最小值为12. (I)设M(x,y),然后对向量条件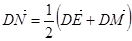 坐标化再化简即可得到所求M的轨迹方程.
坐标化再化简即可得到所求M的轨迹方程.
(II)设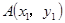 ,
,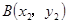 ,
,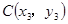 ,
,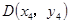 ,,
,,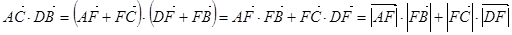
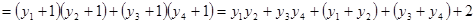
然后再利用直线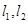 的方程分别与M的轨迹方程联立,消去x,代入上式即可得到关于k的函数关系式,进而利用函数的方法求其最小值
的方程分别与M的轨迹方程联立,消去x,代入上式即可得到关于k的函数关系式,进而利用函数的方法求其最小值
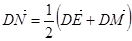 坐标化再化简即可得到所求M的轨迹方程.
坐标化再化简即可得到所求M的轨迹方程.(II)设
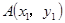 ,
,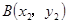 ,
,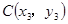 ,
,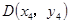 ,,
,,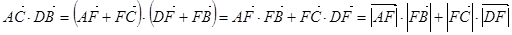
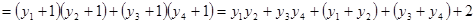
然后再利用直线
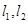 的方程分别与M的轨迹方程联立,消去x,代入上式即可得到关于k的函数关系式,进而利用函数的方法求其最小值
的方程分别与M的轨迹方程联立,消去x,代入上式即可得到关于k的函数关系式,进而利用函数的方法求其最小值
练习册系列答案
相关题目
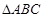 所在平面内一点,且满足
所在平面内一点,且满足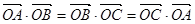 ,则点O是
,则点O是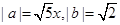 ,且a与b的夹角为
,且a与b的夹角为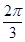 ,若
,若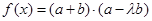
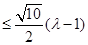
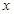 在区间
在区间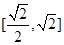 上恒成立,则实数
上恒成立,则实数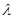 的取值范围是 ( )
的取值范围是 ( )



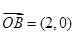 ,
,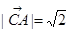 ,
,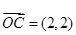 ,则
,则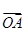 与
与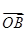 夹角的最小值和最大值依次是 ( )
夹角的最小值和最大值依次是 ( )



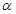 、
、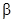 是锐角
是锐角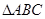 的两个内角,则
的两个内角,则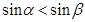 ;(2)在锐角
;(2)在锐角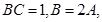 则
则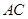 的取值范围为 (
的取值范围为 (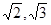 );(3)已知
);(3)已知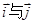 为互相垂直的单位向量,
为互相垂直的单位向量,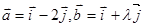 且
且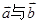 的夹角为锐角,则实数
的夹角为锐角,则实数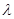 的取值范围是
的取值范围是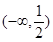 ;(4)已知O是
;(4)已知O是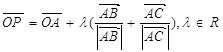 ;(5)直线x= -
;(5)直线x= -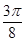 是函数y=sin(2x-
是函数y=sin(2x-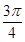 )图象的一条对称轴。其中正确命题是( )
)图象的一条对称轴。其中正确命题是( )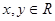 ,
,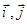 是直角坐标平面内
是直角坐标平面内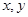 轴正方向上的单位向量,若
轴正方向上的单位向量,若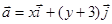 ,
,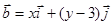 且
且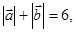 则点
则点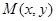 的轨迹是( )
的轨迹是( )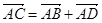 ,
,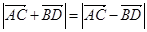 ,则四边形ABCD是
,则四边形ABCD是 中,
中, 所对的边长分别为
所对的边长分别为 ,且
,且 ,
, ,则
,则 。
。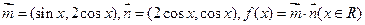 ,
,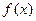 的最小正周期及对称中心;
的最小正周期及对称中心;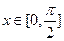 上的值域;
上的值域;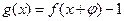 ,若
,若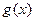 的图像关于原点对称,求
的图像关于原点对称,求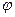 的值。
的值。