题目内容
【题目】如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上.并记组成该“钉”的四条等长的线段公共点为![]() ,钉尖为
,钉尖为![]() .
.

(1)判断四面体![]() 的形状,并说明理由;
的形状,并说明理由;
(2)设![]() ,当
,当![]() 在同一水平面内时,求
在同一水平面内时,求![]() 与平面
与平面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(3)若该“钉”着地后的四个线段根据需要可以调节与底面成角的大小,且保持三个线段与底面成角相同,若![]() ,
,![]() ,问
,问![]() 为何值时,
为何值时,![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
【答案】(1)正四面体;理由见解析(2)![]() ;(3)当
;(3)当![]() 时,最大体积为:
时,最大体积为:![]() ;
;
【解析】
(1)根据线段等长首先确定![]() 为四面体外接球球心;又
为四面体外接球球心;又![]() 底面
底面![]() ,可知
,可知![]() 为正三棱锥;依次以
为正三棱锥;依次以![]() 为顶点均有正三棱锥结论出现,可知四面体棱长均相等,可知其为正四面体;(2)由
为顶点均有正三棱锥结论出现,可知四面体棱长均相等,可知其为正四面体;(2)由![]() 为四面体外接球球心及
为四面体外接球球心及![]() 底面
底面![]() 可得到
可得到![]() 即为所求角;设正四面体棱长为
即为所求角;设正四面体棱长为![]() ,利用
,利用![]() 表示出
表示出![]() 各边,利用勾股定理构造方程可求得
各边,利用勾股定理构造方程可求得![]() ,从而可求得
,从而可求得![]() ,进而得到结果;(3)取
,进而得到结果;(3)取![]() 中点
中点![]() ,利用三线合一性质可知
,利用三线合一性质可知![]() ,从而可用
,从而可用![]() 表示出底面边长和三棱锥的高,根据三棱锥体积公式可将体积表示为关于
表示出底面边长和三棱锥的高,根据三棱锥体积公式可将体积表示为关于![]() 的函数,利用导数求得函数的最大值,并确定此时
的函数,利用导数求得函数的最大值,并确定此时![]() 的取值,从而得到结果.
的取值,从而得到结果.
(1)四面体![]() 为正四面体,理由如下:
为正四面体,理由如下:
![]() 四条线段等长,即
四条线段等长,即![]() 到四面体四个顶点距离相等
到四面体四个顶点距离相等 ![]() 为四面体外接球的球心
为四面体外接球的球心
又![]() 底面
底面![]()
![]() 在底面的射影为
在底面的射影为![]() 的外心
的外心
![]() 四面体
四面体![]() 为正三棱锥,即
为正三棱锥,即![]() ,
,![]()
又任意抛至水平面后,总有一端所在的直线竖直向上,若![]() 竖直向上
竖直向上
可得:![]()
可知四面体![]() 各条棱长均相等
各条棱长均相等 ![]() 为正四面体
为正四面体
(2)由(1)知,四面体![]() 为正四面体,且
为正四面体,且![]() 为其外接球球心
为其外接球球心
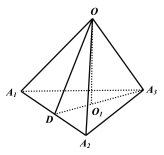
设![]() 中心为
中心为![]() ,则
,则![]() 平面
平面![]() ,如下图所示:
,如下图所示:
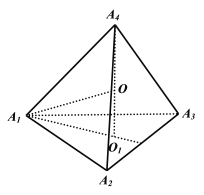
![]() 即为
即为![]() 与平面
与平面![]() 所成角
所成角
设正四面体![]() 棱长为
棱长为![]()
则![]() ,
,![]()
![]() 在
在![]() 中,
中,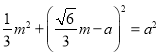 ,解得:
,解得:![]()
![]()
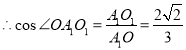
![]()
即![]() 与平面
与平面![]() 所成角为:
所成角为:![]()
(3)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]()
![]() ,
,![]() 为
为![]() 中点
中点 ![]() 且
且![]()
![]() ,
,![]()
![]()
![]()
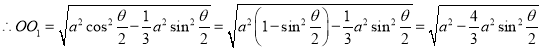
![]()
![]()
令![]() ,
,![]() ,则
,则![]()
设![]() ,
,![]() ,则
,则![]()
令![]() ,解得:
,解得:![]() ,
,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 取极大值,即为最大值:
取极大值,即为最大值:![]()
即当![]() 时,
时,![]() 取得最大值,最大值为:
取得最大值,最大值为:![]()
此时![]() ,即
,即![]()
综上所述,当![]() 时,
时,![]() 体积最大,最大值为:
体积最大,最大值为:![]()

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.367 | 0.329 | 0.308 | 0.290 |
(I)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(II)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸
,则当优等品的尺寸![]() 为何值时,收益
为何值时,收益![]() 的预报值最大? (精确到0.1)
的预报值最大? (精确到0.1)
附:对于样本![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
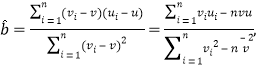
![]()
![]()