题目内容

14．点P（1，4）在直线mx+ny-1=0（m＞0，n＞0）上，则$\frac{1}{m}+\frac{1}{n}$的最小值是（　　）
A．9B．12C．11D．13

分析 由点P在直线mx+ny-1=0（m＞0且n＞0）上，可得m+4n=1，从而有$\frac{1}{m}$+$\frac{1}{n}$=（m+4n）（$\frac{1}{m}$+$\frac{1}{n}$），利用基本不等式的性质解出即可．

解答 解：∵点P在直线mx+ny-1=0（m＞0且n＞0）上，∴m+4n=1．
∴$\frac{1}{m}$+$\frac{1}{n}$=（m+4n）（$\frac{1}{m}$+$\frac{1}{n}$）=5+$\frac{m}{n}$+$\frac{4n}{m}$≥5+2$\sqrt{\frac{m}{n}•\frac{4n}{m}}$=9，当且仅当m=2n时，
即m=$\frac{1}{3}$，n=$\frac{1}{6}$取等号．
∴$\frac{1}{m}$+$\frac{1}{n}$的最小值是29．
故选：A．

点评 熟练掌握指数函数的性质、基本不等式的性质是解题的关键．

练习册系列答案
相关题目
4．若方程2sin（x+$\frac{π}{3}$）=m在[0，π]上有两个不同的实数解，求实数m的取值范围．
5．设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，其中$\overrightarrow{a}$=（cos2x，2sin（$\frac{π}{4}$+x）），$\overrightarrow{b}$=（$\sqrt{3}$，-sin（$\frac{π}{4}$+x）），x∈R．
（1）求函数的单调增区间；
（2）求实数m为何值时，关于x的方程：f（x）+m+2=0在x∈[$\frac{π}{4}$，$\frac{π}{2}$]上有一解，两解？
2．集合A={x|y=lg（1-x）}，B={a|关于x的方程x2-2x+a=0有实解}，则A∩B=（　　）
A．∅B．（-∞，1）C．[0，1）D．（0，1]
9．若函数f（x）=2sin（2x-$\frac{π}{6}$）+1．
（1）求函数f（x）的对称轴和单调递增区间；
（2）若x∈[-$\frac{π}{12}$，$\frac{π}{2}$]时，求函数f（x）的值域．
19．函数f（x）=ax3+bx2+cx+d的部分数值如表：
x-3-2-1012345
f（x）-80-2404001660144
则函数y=lgf（x）的定义域为（-1，1）∪（2，+∞）．
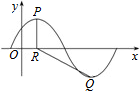6．已知函数f（x）=Asin（$\frac{π}{3}$x+φ），（A＞0，0＜φ＜$\frac{π}{2}$），y=f（x）的部分图象如图所示，P，Q分别为该图象上相邻的最高点和最低点，点P在x轴上的射影为R（1，0），cos∠PRQ=-$\frac{4}{5}$
（1）求A，φ的值；
（2）将函数f（x）的图象上所有的点向右平移θ（θ＞0）个单位，得到函数g（x）的图象，若g（x）在区间[0，3]上单调递增，求θ的最小值
（3）求函数f（x）的单调增区间及对称中心．
3．5名高中毕业生报考三所重点院校，每人限报且只报一所院校，则不同的报名方法有（　　）
A．35种B．53种C．60种D．10种
4．给出下列说法，其中说法正确的序号是②③．
①小于90°的角是第Ⅰ象限角；     ②若α是第Ⅰ象限角，则tanα＞sinα；
③若f（x）=cos2x，|x2-x1|=π，则f（x1）=f（x2）；
④若f（x）=sin2x，g（x）=cos2x，x1、x2是方程f（x）=g（x）的两个根，则|x2-x1|的最小值是π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网