题目内容

（B题）已知圆C的方程为（x-1）2+y2=9，点p为圆上一动点，定点A（-1，0），线段AP的垂直平分线与直线CP交于点M，则为点M的轨迹为（　　）
A．椭圆B．双曲线C．抛物线D．圆
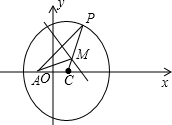
圆C：（x-1）2+y2=9，圆心为（1，0），半径为3，如图，
因为M是线段AP的垂直平分线与CP的交点，所以|MA|=|MP|，
所以|MA|+|MC|=|MC|+|MP|=|PC|=3．
而|AC|=2，|MA|+|MC|＞|AC|．
所以由椭圆定义知，M的轨迹是以A，C为焦点的椭圆．
故选A．
练习册系列答案
相关题目
椭圆的焦点为，点P为其上的动点，当为钝角时，点P横坐标的取值范围是_________；
设定点M1（0，-3），M2（0，3），动点P满足条件|PM1|+|PM2|=a+
9
a
（其中a是正常数），则点P的轨迹是（　　）
A．椭圆B．线段C．椭圆或线段D．不存在
已知F1、F2是两定点，|F1F2|=4，动点M满足|MF1|+|MF2|=4，则动点M的轨迹是（　　）
A．.椭圆B．直线C．圆D．线段
设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点，
（1）设椭圆C上的点（
3
，
3
2
）到F1，F2两点距离之和等于4，写出椭圆C的方程和焦点坐标
（2）设K是（1）中所得椭圆上的动点，求线段KF1的中点B的轨迹方程
（3）设点P是椭圆C上的任意一点，过原点的直线L与椭圆相交于M，N两点，当直线PM，PN的斜率都存在，并记为kPM，KPN试探究kPM•KPN的值是否与点P及直线L有关，并证明你的结论．
求适合下列条件的曲线的标准方程：
（1）a=3b，经过点M（3，0）的椭圆；
（2）a=2
5
，经过点N（2，-5），焦点在y轴上的双曲线．
（Ⅰ）求经过点（-
3
2
，
5
2
），且与椭圆9x2+5y2=45有共同焦点的椭圆方程；
（Ⅱ）已知椭圆以坐标轴为对称轴，且长轴长是短轴长的3倍，点P（3，0）在该椭圆上，求椭圆的方程．
△ABC中，BC=7，AC=3，∠A=120°，求以点B、C为焦点且过点A的椭圆方程．
设是椭圆上的一个点，是椭圆的焦点，如果点到点的距离是，那么点到点的距离是            。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网