题目内容
椭圆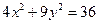 比椭圆焦点在
比椭圆焦点在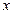 轴上的椭圆
轴上的椭圆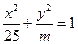 更接近于圆,求
更接近于圆,求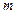 的范围。
的范围。
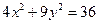 比椭圆焦点在
比椭圆焦点在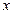 轴上的椭圆
轴上的椭圆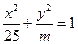 更接近于圆,求
更接近于圆,求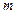 的范围。
的范围。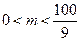
由于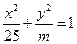 是焦点在
是焦点在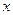 轴上的椭圆,∴
轴上的椭圆,∴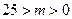 ①,又将
①,又将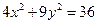 化为标准方程得:
化为标准方程得: ,∴
,∴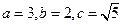 ,∴
,∴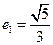 ,又在椭圆
,又在椭圆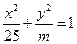 中,
中,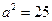 ,
,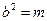 ,
, ,∴
,∴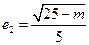 ,由于椭圆
,由于椭圆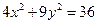 比椭圆焦点在
比椭圆焦点在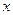 轴上的椭圆
轴上的椭圆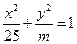 更接近于圆,∴
更接近于圆,∴ ,即
,即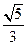
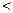
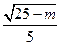 ,解得:
,解得: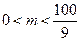 。
。
名师点金:原题可以通过画简图来进行辨别,也可以通过离心率来比较,而变式是利用离心率的大小来求参数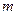 的范围,在求解的过程中还要特别注意作为椭圆,对
的范围,在求解的过程中还要特别注意作为椭圆,对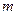 也有限制,故变式是一个新颖的好题,当然也可以这样来变:直接给出两者的离心率的关系,求
也有限制,故变式是一个新颖的好题,当然也可以这样来变:直接给出两者的离心率的关系,求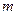 的范围而不用“更接近于圆”这一说法,其实质是一样的。
的范围而不用“更接近于圆”这一说法,其实质是一样的。
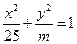 是焦点在
是焦点在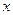 轴上的椭圆,∴
轴上的椭圆,∴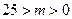 ①,又将
①,又将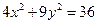 化为标准方程得:
化为标准方程得: ,∴
,∴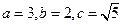 ,∴
,∴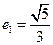 ,又在椭圆
,又在椭圆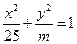 中,
中,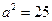 ,
,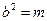 ,
, ,∴
,∴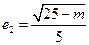 ,由于椭圆
,由于椭圆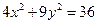 比椭圆焦点在
比椭圆焦点在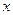 轴上的椭圆
轴上的椭圆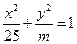 更接近于圆,∴
更接近于圆,∴ ,即
,即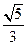
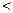
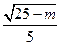 ,解得:
,解得: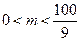 。
。名师点金:原题可以通过画简图来进行辨别,也可以通过离心率来比较,而变式是利用离心率的大小来求参数
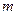 的范围,在求解的过程中还要特别注意作为椭圆,对
的范围,在求解的过程中还要特别注意作为椭圆,对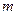 也有限制,故变式是一个新颖的好题,当然也可以这样来变:直接给出两者的离心率的关系,求
也有限制,故变式是一个新颖的好题,当然也可以这样来变:直接给出两者的离心率的关系,求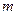 的范围而不用“更接近于圆”这一说法,其实质是一样的。
的范围而不用“更接近于圆”这一说法,其实质是一样的。
练习册系列答案
相关题目
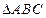 的周长为16,且
的周长为16,且 ,则顶点
,则顶点 的轨迹是( )
的轨迹是( ) ,离心率
,离心率 ,那么它的短轴长是( )
,那么它的短轴长是( )

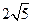

 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为 (1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
(1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。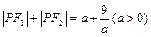 ,则点P的轨迹是( )。
,则点P的轨迹是( )。 是椭圆
是椭圆 的两个焦点,
的两个焦点, =
= ,弦
,弦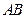 过点
过点 ,则
,则 的周长为( )
的周长为( )
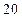


 是椭圆
是椭圆 上的一个点,
上的一个点, 是椭圆的焦点,如果点
是椭圆的焦点,如果点 的距离是
的距离是 ,那么点
,那么点 的距离是 。
的距离是 。