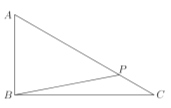
题目内容
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
【答案】(1)见解析;(2)命题为真命题,证明见解析.
【解析】
(1)根据类比推理的基本原则可直接写出结果;
(2)设![]() ,
,![]() ,
,![]() ,表示出直线
,表示出直线![]() 方程后可求得
方程后可求得![]() 点坐标,由此得到
点坐标,由此得到![]() ,同理得到
,同理得到![]() ,根据平面向量的数量积运算可构造方程,结合点
,根据平面向量的数量积运算可构造方程,结合点![]() 在双曲线上可化简得到结果.
在双曲线上可化简得到结果.
(1)类比得命题:若双曲线![]() :
:![]() 交
交![]() 轴于
轴于![]() 两点,点
两点,点![]() 是双曲线
是双曲线![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,则
,则![]() 为定值
为定值![]() .
.
(2)在(1)中类比得到的命题为真命题,证明如下:
不妨设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
∴直线![]() 方程为
方程为![]() .
.
令![]() ,则
,则![]() ,∴点
,∴点![]() 坐标为
坐标为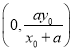 .
.
又![]() ,∴
,∴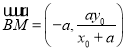 .
.
同法可求得: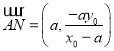 .
.
∴![]() .
.
又∵![]() ,∴
,∴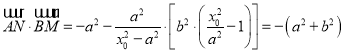 .
.

练习册系列答案
相关题目
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工健康工作,在全校范围内倡导“每天一万步”健步走活动,学校界定一人一天走路不足4千步为健步常人,不少于16千步为健步超人,其他为健步达人,学校随机抽查了36名教职工,其每天的走步情况统计如下:
步数 |
|
|
|
人数 | 6 | 18 | 12 |
现对抽查的36人采用分层抽样的方式选出6人
(1)求从这三类人中各抽多少人;
(2)现从选出的6人中随机抽取2人,求这两人健步类型相同的概率.
【题目】随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
甲班 2 9 1 0 8 2 | 18 17 16 | 乙班 0 0 1 4 7 3 |
(1)判断哪个班的平均身高较高, 并说明理由;
(2)计算甲班的样本方差;
(3)现从乙班这6名学生中随机抽取两名学生,求至少有一名身高不低于![]() 的学生被抽中的概率.
的学生被抽中的概率.