题目内容
【题目】已知方程![]() 恰有四个不同的实数根,当函数
恰有四个不同的实数根,当函数![]() 时,实数K的取值范围是( )
时,实数K的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
利用导数判断![]() 的单调性和极值,得出方程
的单调性和极值,得出方程![]() 的根分布情况,从而得出方程
的根分布情况,从而得出方程![]() 恰有四个不同的实数根等价于关于
恰有四个不同的实数根等价于关于![]() 的方程
的方程![]() 在
在![]() 上有一个解,在
上有一个解,在![]() 上有一个解,利用二次函数的性质列不等式可求出
上有一个解,利用二次函数的性质列不等式可求出![]() 的范围.
的范围.
![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 当
当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
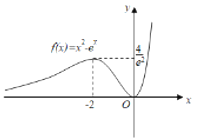
![]() 当
当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,
,
当![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() ,
,
作出![]() 的大致函数图象如图所示,
的大致函数图象如图所示,
令![]() ,则当
,则当![]() 或
或![]() 时,关于
时,关于![]() 的方程
的方程![]() 只有一个解;
只有一个解;
当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有两个解;
有两个解;
当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有三个解,
有三个解,
![]() 恰有四个零点,
恰有四个零点,
![]() 关于
关于![]() 的方程
的方程![]() 在
在![]() 上有一个解,
上有一个解,
在![]() 上有一个解,
上有一个解,
显然![]() 不是方程
不是方程![]() 的解,
的解,
![]() 关于
关于![]() 的方程
的方程![]() 在
在![]() 和
和![]() 上各有一个解,
上各有一个解,
![]() ,解得
,解得![]() ,
,
即实数![]() 的取值范围是
的取值范围是![]() ,故选B.
,故选B.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目