题目内容
已知定义在
的函数
在区间
上的值域为
，
（Ⅰ）求
、
的值；
（Ⅱ）求函数
的最小正周期；
（Ⅲ）求函数的单调减区间.
的函数 在区间上的值域为，（Ⅰ）求
、的值；（Ⅱ）求函数
的最小正周期；（Ⅲ）求函数
的单调减区间.（Ⅰ）、的值分别为3，
（Ⅱ）
（Ⅲ）
、的值分别为3， （Ⅱ） （Ⅲ）试题分析：（Ⅰ）
∵
，∴
，∴
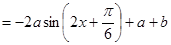
，又
∴
的值域为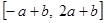
，根据题设条件值域为，故有
，解得
，所以所求、的值分别为3，。（Ⅱ）由（1）得
，∴的最小正周期为
。（Ⅲ）
的单调减区间即为函数
的单调增区间，由
，得
，故
的单调减区间为.点评：本题考查的知识点是三角函数的最值，三角函数的周期性及其求法，其中根据降幂公式（逆用二倍角公式）及辅助角公式，我将函数解析式化为正弦型函数的形式，是解答本题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
.
的值;
的最小正周期及单调递减区间.
(x-6)](x=1，2，3，…，12)来表示，已知6月份的月平均气温最高，为28℃，12月份的月平均气温最低，为18℃，则10月份的平均气温值为_____℃．
的最小正周期及
上的图象.
，
（其中A＞0，
＞0，
＜
的部分图象如图所示，求这个函数的解析式.
．
的最小正周期；
的集合．
，
，函数
的单调递增区间；
都成立，求实数m的最大值.
·
（其中
>o），且函数
的最小正周期为
单位长度，再将所得图象各点的横坐标缩小为原来的
倍（纵坐标不变）得到函数y=g（x）的图象．求函数g（x）的单调区间．