题目内容
已知a,b是单位向量,a·b=0,若向量c满足|c-a-b|=1,则|c|的取值范围是( )
A.[ -1, -1, +1] +1] | B.[ -1, -1, +2] +2] |
C.[1, +1] +1] | D.1, +2 +2 |
A
由题可知a·b=0,则a⊥b.又|a|=|b|=1,且|c-a-b|=1,不妨令c=(x,y),a=(1,0),b=(0,1),则(x-1)2+(y-1)2=1.又|c|=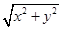 ,所以根据几何关系可知|c|max=
,所以根据几何关系可知|c|max=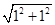 +1=1+
+1=1+ ,|c|min=
,|c|min=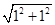 -1=
-1= -1,故选A.
-1,故选A.
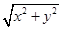 ,所以根据几何关系可知|c|max=
,所以根据几何关系可知|c|max=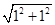 +1=1+
+1=1+ ,|c|min=
,|c|min=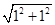 -1=
-1= -1,故选A.
-1,故选A.
练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
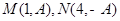 是函数
是函数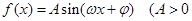 ,
,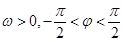 )一个周期内图象上的两点,函数
)一个周期内图象上的两点,函数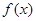 的图象与
的图象与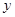 轴交于点
轴交于点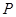 ,满足
,满足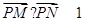 .
.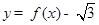 在区间
在区间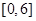 内的零点.
内的零点. =m
=m +n
+n ,且点P落在第Ⅲ部分,则实数m,n满足( )
,且点P落在第Ⅲ部分,则实数m,n满足( )
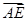 =
=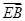 ,
,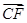 =2
=2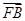 ,联结CE,DF相交于点M,若
,联结CE,DF相交于点M,若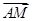 =λ
=λ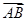 +μ
+μ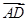 ,则实数λ与μ的乘积为( )
,则实数λ与μ的乘积为( )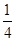
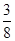
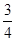

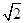 ,则|b|等于________.
,则|b|等于________.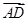 =
=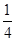 (
( 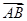 +
+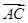 ),
),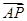 =
=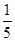
 ,则
,则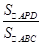 =________.
=________.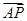 =2
=2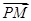 ,则
,则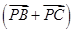 等于( ).
等于( ).

 满足:
满足: ,(
,( )
) ,,则该四边形一定( )
,,则该四边形一定( ) =a,
=a, =b,则
=b,则 =________.
=________.