题目内容
【题目】已知函数![]() 图像上一点
图像上一点![]() 处的切线方程为
处的切线方程为![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在区间
在区间![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围;
的取值范围;
(3)令![]() 如果
如果![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,求证:
,求证:![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据导数的几何意义可知![]() ,利用切线方程求得
,利用切线方程求得![]() ,代入曲线可得关于
,代入曲线可得关于![]() 的方程,与
的方程,与![]() 联立可构造方程组求得结果;(2)将问题转化为
联立可构造方程组求得结果;(2)将问题转化为![]() 与
与![]() 的图象在
的图象在![]() 上有两个交点;利用导数得到
上有两个交点;利用导数得到![]() 在
在![]() 上的单调性和最值,从而确定有两个交点时
上的单调性和最值,从而确定有两个交点时![]() 的取值范围,进而得到结果;(3)采用反证法,假设
的取值范围,进而得到结果;(3)采用反证法,假设![]() ,利用
,利用![]() 在
在![]() 上,中点坐标公式和
上,中点坐标公式和![]() 可化简整理得到
可化简整理得到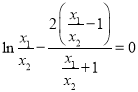 ,令
,令![]() ,构造函数
,构造函数![]() ,利用导数可知
,利用导数可知![]() 在
在![]() 上单调递增,从而得到
上单调递增,从而得到![]() ,与等式矛盾,可知假设不成立,从而证得结论.
,与等式矛盾,可知假设不成立,从而证得结论.
由题意得:![]() 定义域为
定义域为![]() ;
;![]()
(1)![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]()
 ,解得:
,解得:![]()
(2)方程![]() 在区间
在区间![]() 内有两个不等实根等价于
内有两个不等实根等价于![]() 与
与![]() 的图象在
的图象在![]() 上有两个交点
上有两个交点
由(1)知:![]() ,
,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减 ![]()
又![]() ,
,![]()
![]() ,解得:
,解得:![]()
(3)![]() ,则
,则![]()
假设![]() ,则有:
,则有:
![]() …①;
…①;![]() …②;
…②;
![]() …③;
…③;![]() …④
…④
①![]() ②得:
②得:![]()
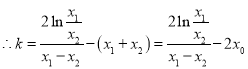
由④得:![]()
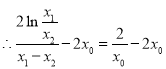 ,即:
,即: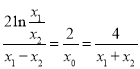
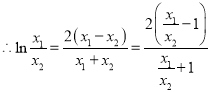 ,即
,即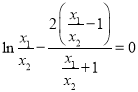
令![]() ,由
,由![]() 得:
得:![]()
设![]() ,
,![]()
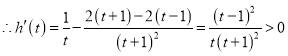
![]() 在
在![]() 上单调递增
上单调递增 ![]()
![]()
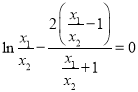 不成立,即假设不成立
不成立,即假设不成立
![]()

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
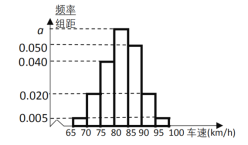
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
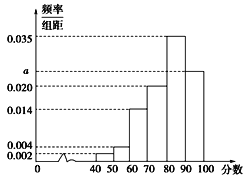
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.