题目内容
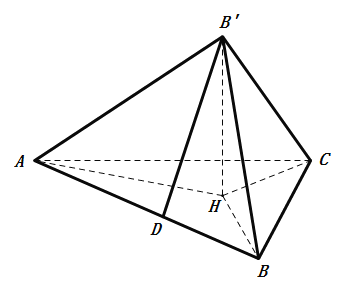
【题目】在直角△ABC中,AC=![]() ,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
,BC=1,点D是斜边AB上的动点,将△BCD沿着CD翻折至△B'CD,使得点B'在平面ACD内的射影H恰好落在线段CD上,则翻折后|AB'|的最小值是_____.
【答案】![]()
【解析】
过点B′作B′H⊥CD于E,连结BH,AH,设∠BCD=∠B′CD=α,则有B′H=sinα,CH=cosα,∠ACE=![]() ﹣α,由此利用余弦定理、勾股定理能求出当α=时,AB′取得最小值.
﹣α,由此利用余弦定理、勾股定理能求出当α=时,AB′取得最小值.
过点B′作B′H⊥CD于H,连结BH,AH,设∠BCD=∠B′CD=α,
则有B′H=sinα,CH=cosα,∠ACH=![]() ﹣α,
﹣α,
在△AHC中,由余弦定理得:
AH2=AC2+CH2﹣2×CH×AC×cos∠ACH=3+cos2α﹣2![]() cosαcos(
cosαcos( ![]() ﹣α)
﹣α)
=3+cos2α﹣2![]() sinαcosα,
sinαcosα,
在Rt△AHB′中,由勾股定理得:
AB'2=AH2+B′H2=3+cos2α﹣2![]() sinαcosα+sin2α=4﹣
sinαcosα+sin2α=4﹣![]() sin2α,
sin2α,
∴当α=![]() 时,AB′取得最小值
时,AB′取得最小值![]() .
.
故答案为:![]() .
.

【题目】2019超长“三伏”来袭,虽然大部分人都了解“伏天”不宜吃生冷食物,但随着气温的不断攀升,仍然无法阻挡冷饮品销量的暴增.现在,某知名冷饮品销售公司通过随机抽样的方式,得到其100家加盟超市3天内进货总价的统计结果如下表所示:
组别(单位:百元) |
|
|
|
|
|
|
频数 | 3 | 11 | 20 | 27 | 26 | 13 |
(1)由频数分布表大致可以认为,被抽查超市3天内进货总价![]() ,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求
,μ近似为这100家超市3天内进货总价的平均值(同一组中的数据用该组区间的中点值作代表),利用正态分布,求![]() ;
;
(2)在(1)的条件下,该公司为增加销售额,特别为这100家超市制定如下抽奖方案:
①令m表示“超市3天内进货总价超过μ的百分点”,其中![]() .若
.若![]() ,则该超市获得1次抽奖机会;
,则该超市获得1次抽奖机会;![]() ,则该超市获得2次抽奖机会;
,则该超市获得2次抽奖机会;![]() ,则该超市获得3次抽奖机会;
,则该超市获得3次抽奖机会;![]() ,则该超市获得4次抽奖机会;
,则该超市获得4次抽奖机会;![]() ,则该超市获得5次抽奖机会;
,则该超市获得5次抽奖机会;![]() ,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
,则该超市获得6次抽奖机会.另外,规定3天内进货总价低于μ的超市没有抽奖机会;
②每次抽奖中奖获得的奖金金额为1000元,每次抽奖中奖的概率为![]() .
.
设超市A参加了抽查,且超市A在3天内进货总价![]() 百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
百元.记X(单位:元)表示超市A获得的奖金总额,求X的分布列与数学期望.
附参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命. 为了研究司机开车时使用手机的情况,交警部门调查了![]() 名机动车司机,得到以下统计:在
名机动车司机,得到以下统计:在![]() 名男性司机中,开车时使用手机的有
名男性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人;在
人;在![]() 名女性司机中,开车时使用手机的有
名女性司机中,开车时使用手机的有![]() 人,开车时不使用手机的有
人,开车时不使用手机的有![]() 人.
人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为开车时使用手机与司机的性别有关;
的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 | 开车时不使用手机 | 合计 | |
男性司机人数 | |||
女性司机人数 | |||
合计 |
(2)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为![]() ,若每次抽检的结果都相互独立,求
,若每次抽检的结果都相互独立,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式与数据:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式
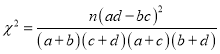 span>,其中
span>,其中![]() .
.