题目内容
2.若x,y满足约束条件:$\left\{\begin{array}{l}{x>0}\\{x+2y≥3}\\{2x+y≤3}\end{array}\right.$;则x-y的取值范围为( )| A. | [0,3] | B. | [0,$\frac{3}{2}$] | C. | [-$\frac{3}{2}$,0] | D. | [-3,0] |
分析 由约束条件作出可行域,令z=x-y,化为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x>0}\\{x+2y≥3}\\{2x+y≤3}\end{array}\right.$作出可行域如图,
令z=x-y,则y=x-z,
联立$\left\{\begin{array}{l}{x+2y=3}\\{2x+y=3}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
∴B(1,1),
又C(0,3),
由图可知,当直线过B时,直线在y轴上的截距最小,z有最大值为0;
当直线过C时,直线在y轴上的截距最大,z有最大值为-3.
∴x-y的取值范围为[-3,0].
故选:D.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.直线y=x+4与曲线y=x2-x+1所围成的封闭图形的面积为( )
| A. | $\frac{22}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{34}{3}$ |
10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
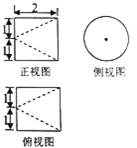

| A. | $\frac{π}{3}$cm3 | B. | $\frac{2π}{3}$cm3 | C. | πcm3 | D. | $\frac{4π}{3}$cm3 |
11. 甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
 甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
甲、乙两名同学8次数学测验成绩如茎叶图所示,$\overline{x}$1,$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1,s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )| A. | $\overline{x}$1>$\overline{x}$2,s1<s2 | B. | $\overline{x}$1=$\overline{x}$2,s1<s2 | C. | $\overline{x}$1=$\overline{x}$2,s1=s2 | D. | $\overline{x}$1<$\overline{x}$2,s1>s2 |
12. 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:
(Ⅰ)若直方图中前三组的频数成等比数列,后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(Ⅲ)在(Ⅱ)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
附:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图直方图:(Ⅰ)若直方图中前三组的频数成等比数列,后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
| 是否近视 年级名次 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(Ⅲ)在(Ⅱ)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$). 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.