题目内容
17.一个四面体的棱长都为1,四个顶点都在同一个球面上,则此球的表面积为$\frac{3π}{2}$.分析 将正四面体补成正方体,通过正方体的对角线与球的半径关系,求解即可.
解答 解:如图,将正四面体补形成一个正方体,正四面体的外接球与正方体的外接球相同.
∵正四面体为1,∴正方体的棱长是$\frac{\sqrt{2}}{2}$,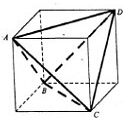
又∵球的直径是正方体的对角线,设球半径是R,
∴2R=$\frac{\sqrt{6}}{2}$
∴R=$\frac{\sqrt{6}}{4}$,球的表面积为4π($\frac{\sqrt{6}}{4}$)2=$\frac{3π}{2}$.
故答案为:$\frac{3π}{2}$.
点评 巧妙构造正方体,利用正方体的外接球的直径为正方体的对角线,从而将问题巧妙转化.若已知正四面体V-ABC的棱长为a,求外接球的半径,我们可以构造出一个球的内接正方体,再应用对角线长等于球的直径可求得.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
8. 已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为( )
已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为( )
 已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为( )
已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
12.设实数x,y满足不等式组$\left\{\begin{array}{l}{x+y+1≥0}\\{x-2y+1≤0}\\{2x-y-1≤0}\end{array}\right.$,则z=2x-3y( )
| A. | 有最大值-1,无最小值 | B. | 有最小值-1,无最大值 | ||
| C. | 最小值-2,最大值3 | D. | 有最小值-2,无最大值 |
2.若x,y满足约束条件:$\left\{\begin{array}{l}{x>0}\\{x+2y≥3}\\{2x+y≤3}\end{array}\right.$;则x-y的取值范围为( )
| A. | [0,3] | B. | [0,$\frac{3}{2}$] | C. | [-$\frac{3}{2}$,0] | D. | [-3,0] |
7.边长为4的正方形ABCD的中心为O,以O为圆心,1为半径作圆,点M是圆O上的任意一点,点N是边AB、BC、CD上的任意一点(含端点),则$\overrightarrow{MN}•\overrightarrow{DA}$的取值范围是( )
| A. | [-18,18] | B. | [-16,16] | C. | [-12,12] | D. | [-8,8] |