Question

4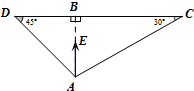．将两个直角三角形如图拼在一起，当E点在线段AB上移动时，若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$，当λ取最大值时，λ-μ的值是$\sqrt{3}$-2．

Answer 1

分析 由题意知，当λ取最大值时，点E与点B重合．△ABC中，由余弦定理求得BC 的值，根据λ=$\frac{DB}{DC}$，μ=$\frac{CB}{CD}$，求出 λ和μ 的值，从而得到λ-μ的值．

解答 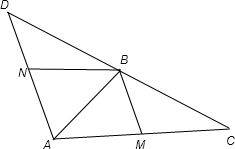解：如图所示：设AM∥BN，且 AM=BN，由题意知，当λ取最大值时，点E与点B重合．△ABC中，由余弦定理
求得BC=$\sqrt{16+64-2×4×8×cos60°}$=4$\sqrt{3}$．
又∵$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$，∴λ=$\frac{AM}{AC}$=$\frac{DB}{DC}$=$\frac{4}{4+4\sqrt{3}}$=$\frac{\sqrt{3}-1}{2}$，
μ=$\frac{AN}{AD}$=$\frac{CB}{CD}$=$\frac{4\sqrt{3}}{4+4\sqrt{3}}$=$\frac{3-\sqrt{3}}{2}$，λ-μ=$\sqrt{3}$-2，
故答案为：$\sqrt{3}$-2．

点评 本题考查余弦定理，两个向量的加减法的法则，以及其几何意义，判断当λ取最大值时，点E与点B重合，是解题的突破口，求出 λ和μ 的值，是解题的关键．