题目内容

20．已知（2x-1）7=a0+a1x+a2x2+…a7x7对任意x的值都成立，求下列各式的值：
（1）a0+a1+a2+…+a7；
（2）a1+a3+a5+a7．

分析 利用特殊值代入法，先求出a0+a1+a2+…+a7的值，再求a1+a3+a5+a7的值．

解答 解：（1）∵（2x-1）7=a0+a1x+a2x2+…+a7x7，
令x=1，得（2×1-1）7=a0+a1+a2+…+a7，
∴a0+a1+a2+…+a7=1；
（2）（2x-1）7=a0+a1x+a2x2+…+a7x7中，
令x=-1，得-37=a0-a1+a2+…-a7x7①，
又1=a0+a1+a2+…+a7②；
②-①，得2（a1+a3+a5+a7）=1+37，
∴a1+a3+a5+a7=$\frac{1{+3}^{7}}{2}$．

点评 本题考查了二项式定理的应用问题，也考查了利用特殊值求值的应用问题，是基础题目．

练习册系列答案
相关题目
10．已知函数f（x）=mx2-mx-1．
（1）若对于x∈R，f（x）＜0恒成立，求实数m的取值范围；
（2）若对于x∈[1，3]，f（x）＜5-m恒成立，求实数m的取值范围．
变式1：将（1）变为：若不等式mx2-mx-1＜0对m∈[1，2]恒成立，求实数x的取值范围．
变式2：将（2）中条件“f（x）＜5-m恒成立”改为“f（x）＜5-m无解”，如何求m的取值范围．
变式3：将（2）条件“f（x）＜5-m恒成立”改为“存在x，使f（x）＜5-m成立”，如何求m的取值范围．
11．求下列对数的值：
（1）log525；
（3）${log}_{\frac{1}{16}}$2：
（5）log7$\root{3}{49}$；
（7）log2（log93）；
（9）${9}^{{log}_{3}2}$．
8．求下列各式中x的值
（1）log5（log3x）=0；
（2）log3（lgx）=1；
（3）ln[log2（lgx）]=0．
15．已知f（x）=πx，x1•x2＞0，试求$\sqrt{f（{x}_{1}）•f（{x}_{2}）}$的值．
5．已知am=2．an=5，求lgam+n的值．
7．在等比数列{an}中，已知a5=3，则a2a5a8等于（　　）
A．6B．9C．27D．3
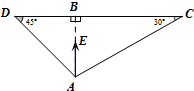4．将两个直角三角形如图拼在一起，当E点在线段AB上移动时，若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$，当λ取最大值时，λ-μ的值是$\sqrt{3}$-2．
5．已知动圆过定点A（0，2），且在x轴上截得的弦长MN=4
（Ⅰ）求动圆的圆心C的轨迹方程L．
（Ⅱ）若A，B为L上的两动点，线段AB过点F（0，1），且$\overrightarrow{AF}$=λ$\overrightarrow{FB}$（λ＞0）．过A、B两点分别作曲线L的切线，设其交点为P．设△ABP的面积为S，求S的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网