题目内容
16.函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f(0),b=f$({\frac{1}{2}})$,c=f(3),则a,b,c的大小关系为c<a<b.分析 判断函数的单调性,然后比较a、b、c的大小.
解答 解:依题意得,当x<1时,f′(x)>0,f(x)为增函数;又f(3)=f(-1),且-1<0<$\frac{1}{2}$<1,因此有f(-1)<f(0)<f$({\frac{1}{2}})$,即有f(3)<f(0)<f$({\frac{1}{2}})$,c<a<b.
故答案为:c<a<b.
点评 本题考查函数的单调性的判断与应用,考查计算能力.

练习册系列答案
相关题目
7.在等比数列{an}中,已知a5=3,则a2a5a8等于( )
| A. | 6 | B. | 9 | C. | 27 | D. | 3 |
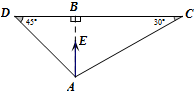 将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.
将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.