题目内容
13.曲线C:$\left\{\begin{array}{l}{x=tanθ}\\{y=\frac{2}{cosθ}}\end{array}\right.$(θ为参数)的焦点坐标是(0,-$\sqrt{5}$),(0,$\sqrt{5}$).分析 化参数方程为普通方程,可知曲线C为焦点在y轴上的双曲线,结合隐含条件求出半焦距,则焦点坐标可求.
解答 解:$\left\{\begin{array}{l}{x=tanθ①}\\{y=\frac{2}{cosθ}②}\end{array}\right.$,
由②得:$\frac{y}{2}$=secθ ③,
③2-②2得$\frac{{y}^{2}}{4}-{x}^{2}=1$.
∴a2=4,b2=1,$c=\sqrt{{a}^{2}+{b}^{2}}=\sqrt{5}$.
∴焦点坐标为(0,-$\sqrt{5}$),(0,$\sqrt{5}$).
故答案为:(0,-$\sqrt{5}$),(0,$\sqrt{5}$).
点评 本题考查参数方程化普通方程,考查了双曲线的简单性质,是基础题.

练习册系列答案
相关题目
2.函数y=2cosx(sinx+cosx)的最大值为( )
| A. | 2 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
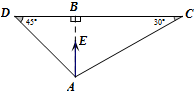 将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.
将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.