题目内容
19.已知函数f(x)=xlnx,g(x)=-x2+ax-3.(Ⅰ) 求f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ) 若存在x∈[$\frac{1}{e}$,e](e是常数,e=2.71828…)使不等式2f(x)≥g(x)成立,求实数a的取值范围;
(Ⅲ) 证明对一切x∈(0,+∞)都有lnx>$\frac{1}{{e}^{x}}$-$\frac{2}{ex}$成立.
分析 (Ⅰ) 对函数求导,根据导函数与0的关系写出函数的单调性和区间,讨论所给的区间和求出的单调区间之间的关系,在不同条件下做出函数的最值.
(Ⅱ) 由题意知2xlnx≥-x2+ax-3,则a≤2lnx+x+$\frac{3}{x}$,设h(x)=2lnx+x+$\frac{3}{x}$(x>0),存在x∈[$\frac{1}{e}$,e],2f(x)≥g(x)恒成立,所以a≤h(x)max,得到结果.
(Ⅲ) 要证明不等式成立,问题等价于证明lxnx>$\frac{x}{{e}^{x}}$-$\frac{2}{e}$(x∈(0,+∞)),由(Ⅰ)知f(x)=xlnx(x∈(0,+∞))的最小值是-$\frac{1}{e}$,构造新函数,得到结论.
解答 解:(Ⅰ) f'(x)=lnx+1,当x∈(0,$\frac{1}{e}$),f'(x)<0,f(x)单调递减,
当x∈($\frac{1}{e}$,+∞),f'(x)>0,f(x)单调递增.
①0<t<t+2<$\frac{1}{e}$,t无解;
②0<t<$\frac{1}{e}$<t+2<$\frac{1}{e}$,即0$<t<\frac{1}{e}$时,f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$;
③$\frac{1}{e}$≤t<t+2,即t≥$\frac{1}{e}$时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt;
∴f(x)min=$\left\{\begin{array}{l}{-\frac{1}{e},0<t<\frac{1}{e}}\\{tlnt.t≥\frac{1}{e}}\end{array}\right.$.
(Ⅱ)由题意知2xlnx≥-x2+ax-3,则a≤2lnx+x+$\frac{3}{x}$,
设h(x)=2lnx+x+$\frac{3}{x}$(x>0),则h′(x)=$\frac{(x+3)(x-1)}{{x}^{2}}$,
x∈[$\frac{1}{e}$,1],h'(x)<0,h(x)单调递减,x∈[1,e],h'(x)>0,h(x)单调递增,
所以h(x)max=max{h($\frac{1}{e}$),h(e)}
因为存在x∈[$\frac{1}{e}$,e],2f(x)≥g(x)恒成立,所以a≤h(x)max;
因为h($\frac{1}{e}$)=-2+$\frac{1}{e}$+3e,h(e)=2+e+$\frac{3}{e}$,
所以h($\frac{1}{e}$)>h(e),
所以a≤-2+$\frac{1}{e}$+3e;
(Ⅲ) 问题等价于证明lxlnx>$\frac{x}{{e}^{x}}$-$\frac{2}{e}$(x∈(0,+∞)),
由(Ⅰ)知f(x)=xlnx(x∈(0,+∞))的最小值是-$\frac{1}{e}$,当且仅当x=$\frac{1}{e}$时取到
设m(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$(x∈(0,+∞)),则m′(x)=$\frac{1-x}{{e}^{x}}$,∴m(x)max=m(1)=-$\frac{1}{e}$,
当且仅当x=1时取到,从而对一切x∈(0,+∞),都有lnx>$\frac{x}{{e}^{x}}$-$\frac{2}{e}$成立.
点评 本题主要考查导数的应用,研究函数单调性、确定函数最值、证明不等式.利用导数研究函数单调性、确定函数最值、证明不等式,是导数的基本应用.这类题解法思路明确,需要细心细致地计算.

| A. | 6 | B. | 9 | C. | 27 | D. | 3 |
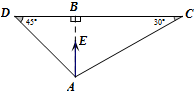 将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.
将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.