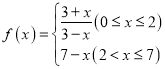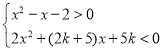Question

【题目】已知函数的导函数为，且对任意的实数都有（是自然对数的底数），且，若关于的不等式的解集中恰有两个负整数，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

首先求得函数的解析式，然后结合函数的单调性和函数的解析式确定函数的性质，最后结合题意求解实数的取值范围即可.

，则，

两侧积分可得：，其中为常数，

令，结合题意可得：，

即函数的解析式为，

据此有：，

令，解得x=l或x=-2，

当x<-2或x>1时，f(x）<0，函数f(x)单调递减，

当-2<x<1时，f(x）>0，函数f(x)单调递减增，

可得：x=1时，函数f(x）取得极大值，x=-2时，函数f(x)取得极小值，

且，，，，，

绘制函数图像如图所示，

观察可得：-e<m≤0时，f(x）-m<0的解集中恰有两个负整数-1，-2.

故m的取值范围是(-e,0].

本题选择C选项.