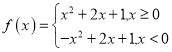题目内容
【题目】如图，已知椭圆C：
(a＞b＞0)的左、右焦点分别为F1、F2，若椭圆C经过点(0，
)，离心率为
，直线l过点F2与椭圆C交于A、B两点．
（1）求椭圆C的方程；
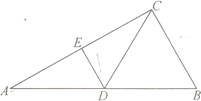
（2）若点N为△F1AF2的内心（三角形三条内角平分线的交点），求△F1NF2与△F1AF2面积的比值；
（3）设点A，F2，B在直线x＝4上的射影依次为点D，G， E．连结AE，BD，试问当直线l的倾斜角变化时，直线AE与BD是否相交于定点T？若是，请求出定点T的坐标；若不是，请说明理由．
【答案】（1）
（2）
（3）见解析.
【解析】分析：（1）由题可得b＝
，
＝
，结合椭圆
可得椭圆方程；（2）因为点N为△F1AF2的内心，所以点N为△F1AF2的内切圆的圆心，然后结合内切圆的半径表示三角形的面积可得面积比值；（3）分直线斜率不存在和斜率存在时两种情况进行讨论，连立方程结合韦达定理求出AE方程得到定点再验证其在BD上即可得到结论.
解：（1）由题意，b＝，又因为＝，所以
＝
，解得a＝2，
所以椭圆C的方程为
＋
＝1.
（2）因为点N为△F1AF2的内心，
所以点N为△F1AF2的内切圆的圆心，设该圆的半径为r.
则
＝
＝
＝
＝
.
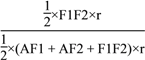（3）若直线l的斜率不存在时，四边形ABED是矩形，
此时AE与BD交于F2G的中点(
，0)，
下面证明：当直线l的倾斜角变化时，直线AE与BD相交于定点T(，0).
设直线l的方程为y＝k(x－1)，
化简得(3＋4k2)x2－8k2x＋4k2－12＝0，
因为直线l经过椭圆C内的点(1，0)，所以△＞0，
设A(x1，y1)，B(x2，y2)，
则x1＋x2＝
，x1x2＝
.
由题意，D(4，y1)，E(4，y2)，
直线AE的方程为y－y2＝
(x－4)，
令x＝，此时y＝y2＋×(－4)＝
＝
＝
＝
＝
＝
＝
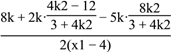
＝0，
所以点T(，0)在直线AE上，
同理可证，点T(，0)在直线BD上.
所以当直线l的倾斜角变化时，直线AE与BD相交于定点T(，0).
名校课堂系列答案
