题目内容
【题目】水培植物需要一种植物专用营养液,已知每投放![]() 且
且![]() 个单位的营养液,它在水中释放的浓度
个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中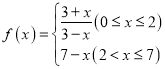 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能持续几天?
(2)若先投放2个单位的营养液,4天后再投放b个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
【答案】(1)4天;(2)![]()
【解析】
(1)营养液有效则需满足y≥4,由分段函数,对x讨论,解不等式即可得到结论;
(2)通过化简、利用基本不等式可知![]() 在[4,7]上恒成立,运用参数分离和换元法,结合基本不等式,即可得到b的最小值.
在[4,7]上恒成立,运用参数分离和换元法,结合基本不等式,即可得到b的最小值.
(1)已知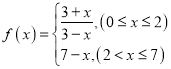 ,当
,当![]() 时,
时,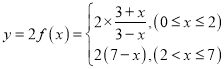
要使营养液有效,则需满足y≥4,则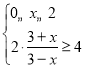 或
或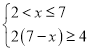 ,
,
即为1≤x≤2或2<x≤5,解得1≤x≤5,所以营养液有效时间可达4天;
(2)当4≤x≤7时,y=14﹣2x+b![]() 在[4,7]上恒成立,
在[4,7]上恒成立,
∴![]() 在[4,7]上恒成立,令
在[4,7]上恒成立,令![]() ,则b≥﹣2(t+
,则b≥﹣2(t+![]() )+20,
)+20,
又﹣2(t+![]() )+20≤﹣2
)+20≤﹣2![]() +20=20﹣
+20=20﹣![]() ,
,
当且仅当t=![]() ,当t=
,当t=![]() 时,即
时,即![]() 时,取等号;
时,取等号;
∵![]() ,∴
,∴![]() ,b的最小值为
,b的最小值为![]() .
.
所以,要使接下来的2天中,营养液能够持续有效,b的最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.