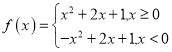题目内容
【题目】已知圆M的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆M相切.
(1)求圆O的方程;
(2)圆O与x轴交于E,F两点,圆O内的动点D使得DE,DO,DF成等比数列,求![]()
![]() 的取值范围.
的取值范围.
【答案】(1)x2+y2=2 (2)[![]() 1,0)
1,0)
【解析】
(1)化简圆M的方程为:x2+y2﹣2x﹣2y﹣6=0,为标准方程,求出圆心和半径,判定圆心O在圆M内部,因而内切,用|MN|=R﹣r,求圆O的方程;
(2)根据圆O与x轴交于E、F两点,圆内的动点D使得|DE|、|DO|、|DF|成等比数列,列出关系,再求![]()
![]() 的取值范围;
的取值范围;
(1)圆M的方程可整理为:(x![]() 1)2+(y-1)2=8,
1)2+(y-1)2=8,
故圆心M(1,1),半径R=2![]() .
.
圆O的圆心为O(0,0),
因为|MO|=![]() <2
<2![]() ,所以点O在圆M内,
,所以点O在圆M内,
故圆O只能内切于圆M.
设其半径为r.因为圆O内切于圆M,
所以有:|MO|=|R-r|,即![]() =|2
=|2![]()
![]() r|,解得r=
r|,解得r=![]() 或r=3
或r=3![]() (舍去);
(舍去);
所以圆O的方程为x2+y2=2.
(2)由题意可知:E(![]()
![]() ,0),F(
,0),F(![]() ,0).
,0).
设D(x,y),由|DE|、|DO|、|DF|成等比数列,
得|DO|2=|DE|×|DF|,
即:![]() ×
×![]() =x2+y2,
=x2+y2,
整理得:x2![]() y2=1.
y2=1.
![]()
![]() =(
=(![]()
![]() ,
,![]() y)(
y)(![]() ,
,![]() y)=x2+y2
y)=x2+y2![]() 2=2y2
2=2y2![]() 1,
1,
由于点D在圆N内,
故有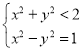 ,由此得y2<
,由此得y2<![]() ,
,
∴![]()
![]() 的取值范围是[
的取值范围是[![]() 1,0).
1,0).

练习册系列答案
相关题目