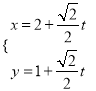题目内容
【题目】设![]() 、
、![]() 为平面上两个点集,满足
为平面上两个点集,满足![]() ,
,![]() ,且任意三点不共线.在集合
,且任意三点不共线.在集合![]() 和
和![]() 间各连若干条线段,每条线段均一个端点在集合
间各连若干条线段,每条线段均一个端点在集合![]() 中,另一个端点在集合
中,另一个端点在集合![]() 中,且任意两点间至多连一条线段,记所有线段构成的集合为
中,且任意两点间至多连一条线段,记所有线段构成的集合为![]() .若集合
.若集合![]() 满足对于集合
满足对于集合![]() 或
或![]() 中任意一点均至少连出
中任意一点均至少连出![]() 条线段,则称集合
条线段,则称集合![]() 是“
是“![]() 一好的”.试确定
一好的”.试确定![]() 的最大值,使得去掉任意一条线段,集合
的最大值,使得去掉任意一条线段,集合![]() 均不是
均不是![]() 一好的.
一好的.
【答案】见解析
【解析】
设集合![]() 中有
中有![]() 个点引出边数不为
个点引出边数不为![]() 条,有
条,有![]() 个点恰引出
个点恰引出![]() 条边,设集合
条边,设集合![]() 中有
中有![]() 个点引出边数不为
个点引出边数不为![]() 条,有
条,有![]() 个点恰引出
个点恰引出![]() 条边.
条边.
由于对称性,不妨设![]() .
.
记![]() ,其中,
,其中,![]() 为集合
为集合![]() 中所有恰引出
中所有恰引出![]() 条线段的点构成的集合,
条线段的点构成的集合,![]() 为集合
为集合![]() 中除去
中除去![]() 外余下的点构成的集合,记B=
外余下的点构成的集合,记B=![]() ,其中,
,其中,![]() 为集合
为集合![]() 中所有恰引出
中所有恰引出![]() 条线段的点构成的集合,
条线段的点构成的集合,![]() 为集合
为集合![]() 中除去
中除去![]() 外余下的点构成的集合.
外余下的点构成的集合.
则![]() 满足以下两个估计:
满足以下两个估计:
(1) ![]() .
.
注意到,集合![]() 中的点仅能与集合
中的点仅能与集合![]() 中的点相邻,故对于
中的点相邻,故对于![]() ,
,
![]() .
.
(2)![]() .
.
对于集合![]() 中的任意一条边,至少有一个端点在集合
中的任意一条边,至少有一个端点在集合![]() 或
或![]() 内,因此,
内,因此,
![]() .
.
由(1)、(2)知
![]()
![]() .
.
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() .
.
故当![]() 时,
时,
![]() ;
;
当![]() 时,
时,![]() ,即
,即
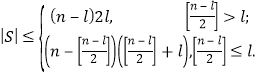
构造:(i)若![]() ,构造两个完全的二部图
,构造两个完全的二部图![]() ,即将集合
,即将集合![]() 中的点划分为两个集合
中的点划分为两个集合![]() 、
、![]() ;将集合
;将集合![]() 中的点划分为两个集合
中的点划分为两个集合![]() 、
、![]() ,
,![]() ,其中,将集合
,其中,将集合![]() 中每一点与集合
中每一点与集合![]() 中每一点均连线,将集合
中每一点均连线,将集合![]() 中每一点和集合
中每一点和集合![]() 中每一点均连线.
中每一点均连线.
(ii)若![]() ,对集合
,对集合![]() 、
、![]() 进行如下的划分:
进行如下的划分:
![]() ,
,
![]() ,
,![]() ;
;
![]() ,
,
![]() ,
,![]() .
.
此时,将集合![]() 中的每一点与集合
中的每一点与集合![]() 中的每一点相连,将集合
中的每一点相连,将集合![]() 中的每一点与集合
中的每一点与集合![]() i中的每一点均相连.然后,在
i中的每一点均相连.然后,在![]() 和
和![]() 这两个点集间再构造一个
这两个点集间再构造一个![]() 的二部正则图即可.
的二部正则图即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目