题目内容
8.已知正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与A1B1所成角的余弦值为$\frac{1}{3}$.分析 由A1B1∥AB,得∠BAE是异面直线AE与A1B1所成角,由此利用余弦定理能求出结果.
解答 解: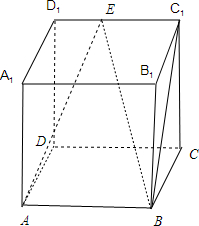 连结AE、BE、BC1,
连结AE、BE、BC1,
∵A1B1∥AB,∴∠BAE是异面直线AE与A1B1所成角,
设正方体ABCD-A1B1C1D1的棱长为2,
∵E为C1D1的中点,
∴AE=BE=$\sqrt{B{{C}_{1}}^{2}+E{{C}_{1}}^{2}}$=$\sqrt{8+1}$=3,AB=2,
∴cos∠BAE=$\frac{A{B}^{2}+A{E}^{2}-B{E}^{2}}{2AB•AE}$=$\frac{4+9-9}{2×2×3}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
17.某公司筹备展览会的各项工作具体如下表:
(1)分析以上各项工作之间的先后关系;
(2)画出流程图并计算最短总工期.
| 工作代码 | 工作名称 | 持续天数 |
| A | 张贴广告、收集作品 | 7 |
| B | 购买展览品 | 3 |
| C | 布置展厅 | 4 |
| D | 展品布置 | 5 |
| E | 宣传语与环境布置 | 2 |
| F | 展前检查 | 2 |
(2)画出流程图并计算最短总工期.