题目内容
20.已知直线l:y=x+m交椭圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1于不同的A、B两点,求|AB|的最大值.分析 将直线方程代入椭圆方程,运用韦达定理和弦长公式,化简整理,即可得到最大值.
解答 解:设l:y=x+m,代入$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1,
整理得5x2+6mx+3m2-6=0,
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{6m}{5}$,x1x2=$\frac{3{m}^{2}-6}{5}$,
|AB|=$\sqrt{2}$•|x1-x2|
=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}$•$\sqrt{\frac{36{m}^{2}}{25}-\frac{12{m}^{2}-24}{5}}$=$\frac{\sqrt{2}}{5}$•$\sqrt{120-24{m}^{2}}$.
由△>0,得36m2-20(3m2-6)>0,
解得m2<5,
∴当m=0时,|AB|max=$\frac{4\sqrt{15}}{5}$.
点评 本题考查椭圆弦长最大值的求法,解题时要注意弦长公式的运用,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知直线l:x-y+4=0与圆C:(x-1)2+(y-1)2=2,则C上各点到l距离的最小值为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
12.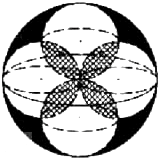 如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.v1为小球相交部分(图中阴影部分)的体积,v2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )
如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.v1为小球相交部分(图中阴影部分)的体积,v2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )
 如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.v1为小球相交部分(图中阴影部分)的体积,v2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )
如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.v1为小球相交部分(图中阴影部分)的体积,v2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )| A. | v1=$\frac{v}{2}$ | B. | v2=$\frac{v}{2}$ | C. | v1>v2 | D. | v1<v2 |
9.已知点P的柱坐标为($\sqrt{2}$,$\frac{π}{4}$,5),点B的球坐标为($\sqrt{6}$,$\frac{π}{3}$,$\frac{π}{6}$),则这两个点在空间直角坐标系中的点的坐标为( )
| A. | 点P(5,1,1),点B($\frac{3\sqrt{6}}{4}$,$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{6}}{2}$) | B. | 点P(1,1,5),点B($\frac{3\sqrt{6}}{4}$,$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{6}}{2}$) | ||
| C. | 点P($\frac{3\sqrt{6}}{4}$,$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{6}}{2}$),点P(1,1,5) | D. | 点P(1,1,5),点B($\frac{\sqrt{6}}{2}$,$\frac{3\sqrt{6}}{4}$,$\frac{3\sqrt{2}}{4}$) |