题目内容
【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 证明:Tn+12=﹣2an+10bn(n∈N*).
【答案】
(1)解:设等差数列的公差为d,等比数列的公比为q,
由a1=b1=2,得a4=2+3d,b4=2q3,s4=8+6d,
由条件a4+b4=27,s4﹣b4=10,
得方程组 ![]() ,解得
,解得 ![]() ,
,
故an=3n﹣1,bn=2n,n∈N*.
(2)证明:方法一,由(1)得,Tn=2an+22an﹣1+23an﹣2+…+2na1; ①;
2Tn=22an+23an﹣1+…+2na2+2n+1a1; ②;
由②﹣①得,Tn=﹣2(3n﹣1)+3×22+3×23+…+3×2n+2n+2
= ![]() +2n+2﹣6n+2
+2n+2﹣6n+2
=10×2n﹣6n﹣10;
而﹣2an+10bn﹣12=﹣2(3n﹣1)+10×2n﹣12=10×2n﹣6n﹣10;
故Tn+12=﹣2an+10bn(n∈N*).
方法二:数学归纳法,
③当n=1时,T1+12=a1b1+12=16,﹣2a1+10b1=16,故等式成立,
④假设当n=k时等式成立,即Tk+12=﹣2ak+10bk,
则当n=k+1时有,
Tk+1=ak+1b1+akb2+ak﹣1b3+…+a1bk+1
=ak+1b1+q(akb1+ak﹣1b2+…+a1bk)
=ak+1b1+qTk
=ak+1b1+q(﹣2ak+10bk﹣12)
=2ak+1﹣4(ak+1﹣3)+10bk+1﹣24
=﹣2ak+1+10bk+1﹣12.
即Tk+1+12=﹣2ak+1+10bk+1,因此n=k+1时等式成立.
③④对任意的n∈N*,Tn+12=﹣2an+10bn成立.
【解析】(1)直接设出首项和公差,根据条件求出首项和公差,即可求出通项.(2)先写出Tn的表达式;方法一:借助于错位相减求和;
方法二:用数学归纳法证明其成立.
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对等比数列的通项公式(及其变式)的理解,了解通项公式:
,以及对等比数列的通项公式(及其变式)的理解,了解通项公式:![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
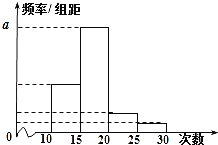
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
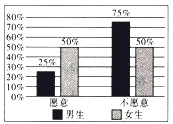
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.
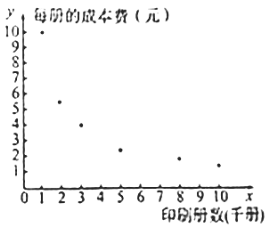
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: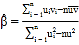 ,
,![]() .
.
