题目内容
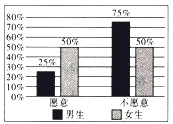
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?
愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.
【答案】(1) 没有99%的把握认为愿意参与志愿活动与性别有关(2) ![]()
【解析】试题分析:(1)完善![]() 列联表,求出
列联表,求出![]() ,然后判断是否有
,然后判断是否有![]() 的把握认为愿意参与志愿活动与性别有关;
的把握认为愿意参与志愿活动与性别有关;
(2)分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,则女生4人,男生3人,分别编号为![]() 从中任取两人的所有基本事件共有21种情况,其中满足两人中至少有一人是女生的基本事件数有18个,从而求得抽取的2人至少有一名女生的概率.
从中任取两人的所有基本事件共有21种情况,其中满足两人中至少有一人是女生的基本事件数有18个,从而求得抽取的2人至少有一名女生的概率.
试题解析:
(Ⅰ)
愿意 | 不愿意 | 总计 | |
男生 | 15 | 45 | 60 |
女生 | 20 | 20 | 40 |
总计 | 35 | 65 | 100 |
计算![]() ,
,
所以没有99%的把握认为愿意参与志愿活动与性别有关.
(Ⅱ)用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,则女生4人,男生3人,分别编号为![]() 从中任取两人的所有基本事件如下:
从中任取两人的所有基本事件如下:![]()
![]() ,
,![]() ,
,![]()
![]() ,共有21种情况,其中满足两人中至少有一人是女生的基本事件数有
,共有21种情况,其中满足两人中至少有一人是女生的基本事件数有![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】设有直线![]() 和平面
和平面![]() ,则下列四个命题中,正确的是( )
,则下列四个命题中,正确的是( )
A. 若m∥α,n∥α,则m∥nB. 若mα,nα,m∥β,l∥β,则α∥β
C. 若α⊥β,mα,则m⊥βD. 若α⊥β,m⊥β,mα,则m∥α
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级![]() 名学生中进行了抽样调查,发现喜欢甜品的占
名学生中进行了抽样调查,发现喜欢甜品的占![]() .这
.这![]() 名学生中南方学生共
名学生中南方学生共![]() 人。南方学生中有
人。南方学生中有![]() 人不喜欢甜品.
人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有![]() 名数学系的学生,其中
名数学系的学生,其中![]() 名不喜欢甜品;有
名不喜欢甜品;有![]() 名物理系的学生,其中
名物理系的学生,其中![]() 名不喜欢甜品.现从这两个系的学生中,各随机抽取
名不喜欢甜品.现从这两个系的学生中,各随机抽取![]() 人,记抽出的
人,记抽出的![]() 人中不喜欢甜品的人数为
人中不喜欢甜品的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |