题目内容
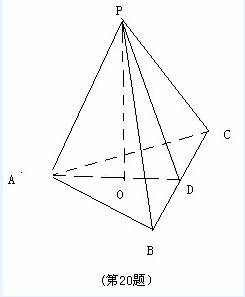
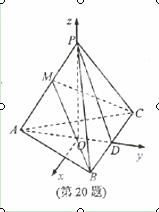
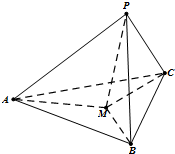
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(Ⅰ)证明:AP⊥BC;
(Ⅱ)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
【答案】
本题主要考查空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查想象能力和运算求解能力。满分15分。
方法以:
(Ⅰ)证明:如图,以O为原点,以射线OP为z轴的正半轴,建立空间直角坐标系O-xyz
则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0)
P(0,0,4)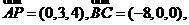 由此可得
由此可得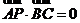 所以
所以
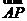 ⊥
⊥ ,即AP⊥BC.
,即AP⊥BC.
(Ⅱ)解:设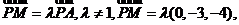
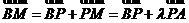
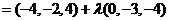
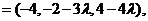
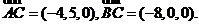
设平面BMC的法向量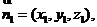
平面APC的法向量
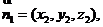
由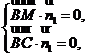
得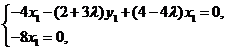
即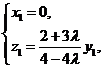 可取
可取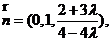
由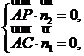 即
即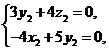 得
得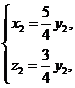 可取
可取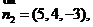
由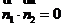 ,得
,得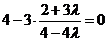
解得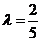 ,故AM=3
,故AM=3
综上所述,存在点M符合题意,AM=3。
方法二:
(Ⅰ)证明:由AB=AC,D是BC的中点,得AD⊥BC,
又PO⊥平面ABC,得PO⊥BC。
因为PO∩BC=0,所以BC⊥平面PAD
故BC⊥PA.
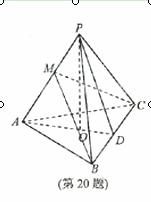 (Ⅱ)解:如图,在平面PAD内作BM⊥PA于M,连CM.
(Ⅱ)解:如图,在平面PAD内作BM⊥PA于M,连CM.
由(Ⅰ)中知AP⊥BC,得AP⊥平面BMC.
又AP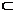 平面APC,所以平面BMC⊥平面APC。
平面APC,所以平面BMC⊥平面APC。
在Rt⊿ADB中,AB2=AD2+BD2=41,得AB=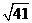
在Rt⊿POD中, PB2=PO2+OD2,
在Rt⊿PDB中, PB2=PD2+BD2,
所以PB2=PO2+OD2+BD2=36,得PB=6.
在Rt⊿POA中, PA2=AO2+OP2=25,得PA=5
又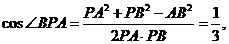
从而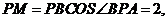 所以
所以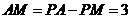
综上所述,存在点M符合题意,AM=3.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是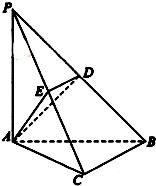 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱