题目内容
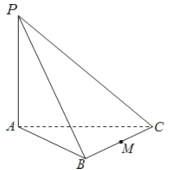
【题目】如图,三棱锥![]() 中,
中,![]() 底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为
底面ABC,M是 BC的中点,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为![]() . 求:
. 求:
(1)三棱锥![]() 的体积;
的体积;
(2)异面直线PM与AC所成角的大小. (结果用反三角函数值表示)
【答案】(1)2;(2)![]() .
.
【解析】
试题(1)欲求三棱锥P-ABC的体积,只需求出底面积和高即可,因为底面ABC是边长为2的正三角形,所以底面积可用![]() 来计算,其中a是正三角形的边长,又因为PA⊥底面ABC,所以三棱锥的高就是PA长,再代入三棱锥的体积公式即可.(2)欲求异面直线所成角,只需平移两条异面直线中的一条,是它们成为相交直线即可,由M为BC中点,可借助三角形的中位线平行于第三边的性质,做出
来计算,其中a是正三角形的边长,又因为PA⊥底面ABC,所以三棱锥的高就是PA长,再代入三棱锥的体积公式即可.(2)欲求异面直线所成角,只需平移两条异面直线中的一条,是它们成为相交直线即可,由M为BC中点,可借助三角形的中位线平行于第三边的性质,做出![]() 的中位线,就可平移BC,把异面直线所成角转化为平面角,再放入
的中位线,就可平移BC,把异面直线所成角转化为平面角,再放入![]() 中,求出角即可.
中,求出角即可.
试题解析:(1)因为![]() 底面
底面![]() ,
,![]() 与底面
与底面![]() 所成的角为
所成的角为![]()
所以![]() , 因为
, 因为![]() ,所以
,所以![]()
![]()
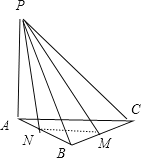
(2)连接![]() ,取
,取![]() 的中点,记为
的中点,记为![]() ,连接
,连接![]() ,则
,则![]()
所以![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角
所成的角
计算可得:![]() ,
,![]() ,
,![]()
![]()
异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.

练习册系列答案
相关题目

