题目内容
17.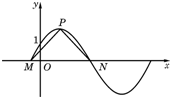 如图,函数y=2sin($\frac{π}{2}$x+φ) x∈R,其中0≤φ≤$\frac{π}{2}$的图象与y轴交于点(0,1).
如图,函数y=2sin($\frac{π}{2}$x+φ) x∈R,其中0≤φ≤$\frac{π}{2}$的图象与y轴交于点(0,1).(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求$\overrightarrow{PM}$和$\overrightarrow{PN}$的夹角的余弦值.
分析 (Ⅰ)根据函数图象过点点(0,1),求得sinφ的值,可得φ的值.
(Ⅱ)由条件求得M、N、P的坐标,再根据cos<$\overrightarrow{PM}$,$\overrightarrow{PN}$>=$\frac{\overrightarrow{PM}•\overrightarrow{PN}}{|\overrightarrow{PM}|•|\overrightarrow{PN}|}$,计算求得结果.
解答 解:( I)因为函数图象过点点(0,1),所以2sinφ=1,即sinφ=$\frac{1}{2}$.
因为0≤φ≤$\frac{π}{2}$,所以φ=$\frac{π}{6}$.
( II)由函数及其图象,得M(-$\frac{1}{3}$,0)、N ($\frac{5}{3}$,0)、P($\frac{2}{3}$,2),
所以$\overrightarrow{PM}$=(-1,-2)、$\overrightarrow{PN}$=(1,-2),
从而cos<$\overrightarrow{PM}$,$\overrightarrow{PN}$>=$\frac{\overrightarrow{PM}•\overrightarrow{PN}}{|\overrightarrow{PM}|•|\overrightarrow{PN}|}$=$\frac{-1+4}{\sqrt{5}•\sqrt{5}}$=$\frac{3}{5}$.
点评 本题主要考查正弦函数的图象特征,用两个向量的数量积表示两个向量的夹角,属于基础题.

练习册系列答案
相关题目
5.“|x-1|<2成立”是“(x+2)(x-3)<0成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.已知复数z=$\frac{2}{1+\sqrt{3}i}$,则|$\overline{z}$|等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | 1 | D. | $\sqrt{2}$ |
9.下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
若两个量间的回归直线方程为$\widehat{y}$=1.16x+a,则a的值为( )
| 身高 | 170 | 171 | 166 | 178 | 160 |
| 体重 | 75 | 80 | 70 | 85 | 65 |
| A. | -122.2 | B. | -121.04 | C. | -91 | D. | -92.3 |
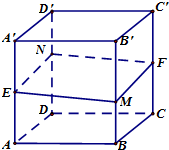 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论: