题目内容

13．经过两点Q（1，1），P（4，3）的直线的参数方程，如果应用共线向量的充要条件来求，方程和参数的含义分别是x，y均为λ的一次函数，|λ|即为两向量的长度的比．

分析 设所求直线上任一点M为（x，y），由向量共线的充要条件可得$\overrightarrow{PM}$=λ$\overrightarrow{PQ}$，由坐标表示即可得到．

解答 解：设所求直线上任一点M为（x，y），
由向量共线的充要条件可得
$\overrightarrow{PM}$=λ$\overrightarrow{PQ}$，
即为（x-4，y-3）=λ（1-4，1-3），
即有直线的参数方程为$\left\{\begin{array}{l}{x=4-3λ}\\{y=3-2λ}\end{array}\right.$，λ为参数．
故答案为：x，y均为λ的一次函数，|λ|即为两向量的长度的比．

点评 本题考查直线的参数方程的求法，同时考查向量共线定理的运用，属于基础题．

练习册系列答案
相关题目
3．已知等差数列{an}的公差d≠0，若a1，a3，a9成等比数列，那么公比为（　　）
A．$\frac{1}{3}$B．3C．$\frac{1}{2}$D．2
4．设数列满足a1=3，（2-an）•an+1=1，则数列{an}的通项公式是an=$\frac{2n-5}{2n-3}$．
1．平行四边形ABCD中心为O，P为该平向任一点，且$\overrightarrow{PO}$=$\overrightarrow{a}$，则$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\overrightarrow{PD}$=4$\overrightarrow{a}$．
8．已知sin（$\frac{π}{2}$+θ）+cos（$\frac{π}{2}$-θ）=-$\frac{1}{5}$，θ∈（0，π），求tanθ
18．等差数列{an}中，若a15=10，a47=90，则a2+a4+…+a60=1500．
3．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，P是椭圆上异于顶点的动点，若恰好有4个不同的点P，使得△PF1F2为等腰三角形，且有一个角为钝角，则椭圆的离心率的取值范围是（$\frac{1}{3}$，$\sqrt{2}-1$）．
20．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，右顶点为A，点M（a，b）满足MF2平分∠F1MA那么椭圆的离心率为$\frac{1}{2}$．
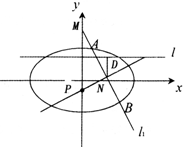1．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的长轴长是短轴长的$\sqrt{3}$倍，且经过点（$\sqrt{3}$，1）．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设点M（0，2），直线l：y=1，过M任作一条不与y轴重合的直线l1，与椭圆相交于A、B两点，过AB的中点N作直线l2与y轴交于点P，D为N在直线l上的射影，若|AB|2=4|ND|•|MP|，求直线l2的斜率的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网