题目内容
1.平行四边形ABCD中心为O,P为该平向任一点,且$\overrightarrow{PO}$=$\overrightarrow{a}$,则$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\overrightarrow{PD}$=4$\overrightarrow{a}$.分析 可画出图形,根据图形及向量加法便有$\overrightarrow{PA}=\overrightarrow{PO}+\overrightarrow{OA}$,$\overrightarrow{PB}=\overrightarrow{PO}+\overrightarrow{OB}$,$\overrightarrow{PC}=\overrightarrow{PO}+\overrightarrow{OC}$,$\overrightarrow{PD}=\overrightarrow{PO}+\overrightarrow{OD}$,而$\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$,从而求出答案.
解答 解:如图,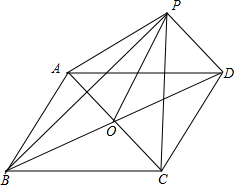 $\overrightarrow{PA}=\overrightarrow{PO}+\overrightarrow{OA}$,$\overrightarrow{PB}=\overrightarrow{PO}+\overrightarrow{OB}$,$\overrightarrow{PC}=\overrightarrow{PO}+\overrightarrow{OC}$,$\overrightarrow{PD}=\overrightarrow{PO}+\overrightarrow{OD}$;
$\overrightarrow{PA}=\overrightarrow{PO}+\overrightarrow{OA}$,$\overrightarrow{PB}=\overrightarrow{PO}+\overrightarrow{OB}$,$\overrightarrow{PC}=\overrightarrow{PO}+\overrightarrow{OC}$,$\overrightarrow{PD}=\overrightarrow{PO}+\overrightarrow{OD}$;
∴$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}=4\overrightarrow{PO}=4\overrightarrow{a}$.
故答案为:4$\overrightarrow{a}$.
点评 考查向量加法的几何意义,平行四边形对角线互相平分,相反向量的概念.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
| A. | 范围相同 | B. | 顶点坐标相同 | C. | 焦点坐标相同 | D. | 离心率相同 |