题目内容
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=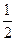 PD。
PD。
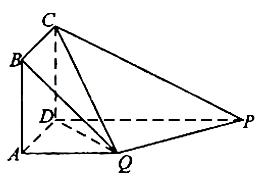
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
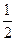 PD。
PD。
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
解析:(I)由条件知,PDAQ是直角梯形,
因为AQ⊥平面ABCD,所以平面PDAQ⊥平面ABCD,交线是AD。
又四边形ABCD是正方形,DC⊥AD,所以DC⊥平面PDAQ,可得PQ⊥DC。
在直角梯形PDAQ中可得DQ=PQ=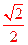 PD,则PQ⊥QD.
PD,则PQ⊥QD.
所以PQ⊥平面PCQ.
(2 )设AB=a
因为AQ⊥平面ABCD,所以平面PDAQ⊥平面ABCD,交线是AD。
又四边形ABCD是正方形,DC⊥AD,所以DC⊥平面PDAQ,可得PQ⊥DC。
在直角梯形PDAQ中可得DQ=PQ=
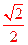 PD,则PQ⊥QD.
PD,则PQ⊥QD.所以PQ⊥平面PCQ.
(2 )设AB=a
由题设知AQ 为棱锥Q-ABCD 的高, 所以棱锥Q-ABCD 的体积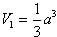
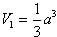
由(1 )知PQ 为棱锥P-DCQ 的高,而PQ=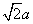 ,
,
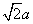 ,
, △DCQ 的面积为 ,
,
 ,
, 所以棱锥P-DCQ 的体积为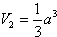
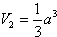
故棱锥Q-ABCD 的体积与棱锥P-DCQ 的体积的比值为1 。
略

练习册系列答案
相关题目
 的侧面
的侧面 是菱形,
是菱形, 。
。 ;
; 上的点且
上的点且 ,求
,求 的值。
的值。
 中,平面
中,平面 侧面
侧面 .
. ;
; 与平面
与平面 所成角是
所成角是 ,锐二面角
,锐二面角 的平面角是
的平面角是 ,试判断
,试判断
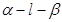 为
为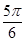 ,直线
,直线 ,直线
,直线 ,则直线
,则直线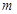 与
与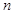 所成角的范围是
所成角的范围是 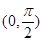

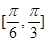
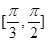
 中,
中,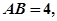 沿对角线
沿对角线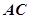 将正方形
将正方形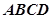 折成一个直二面角
折成一个直二面角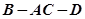 ,则点
,则点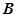 到直线
到直线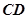 的距离为( )
的距离为( )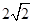
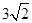
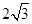
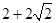
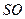 中,
中,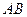 、
、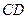 为底面圆的两条直径,
为底面圆的两条直径,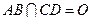 ,且
,且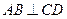 ,
,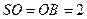 ,
,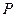 为
为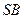 的中点.异面直线
的中点.异面直线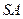 与
与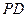 所成角的正切值为 .
所成角的正切值为 .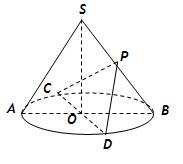
 过点
过点 ,且
,且 是它的一个法向量,则
是它的一个法向量,则 (本小题满分12分)
(本小题满分12分)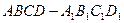 的下底面
的下底面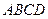 是边长为
是边长为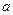 的正方形,
的正方形,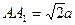 ,且点
,且点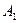 在下底面
在下底面 点.
点.
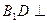 面
面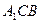 ;
; 的大小.
的大小.