题目内容
【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π
【答案】B
【解析】解:∵E、F分别是AC,PC的中点,∴EF∥PA,
∵P﹣ABC是正三棱锥,∴PA⊥BC(对棱垂直),
∴EF⊥BC,又EF⊥BF,且BF∩BC=B,
∴EF⊥平面PBC,∴PA⊥平面PBC,
∴∠APB=∠APC=∠BPC=90°,
以PA、PB、PC为从同一点P出发的正方体三条棱,
将此三棱锥补成正方体,如图所示:
∵三棱锥和正方体有相同的外接球,
∴正方体的体对角线就是外接球的直径,
又AB=2,∴PA= ![]() ,∴2R=
,∴2R= ![]() ,则R=
,则R= ![]() ,
,
∴三棱锥P﹣ABC的外接球的表面积为:4πR2=4π× ![]() =6π,
=6π,
故选B.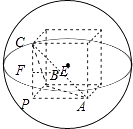

练习册系列答案
相关题目
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: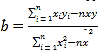 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()