Question

【题目】若a，b在区间 上取值，则函数 在R上有两个相异极值点的概率是（ ）
A.
B.1-
C.
D.

Answer 1

【答案】C
【解析】解：易得f′（x）=ax2+2bx+ a，
函数f（x）在R上有两个相异极值点的充要条件：
是a≠0且其导函数的判别式大于0，即a≠0且4b2﹣a2＞0，
又a，b在区间[0， ]上取值，则a＞0，b＞ a，
点（a，b）满足的区域如图中阴影部分所示，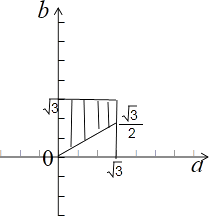

其中正方形区域的面积为3，
阴影部分的面积为3﹣ = ，
故所求的概率p= = ，
故选：C．
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案，需要熟知求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．