题目内容
5.函数f(x)=${x}^{{m}^{2}+m-2}$在第一象限为减函数,则m的取值范围是(-2,1).分析 根据幂函数的性质进行求解即可.
解答 解:∵f(x)=${x}^{{m}^{2}+m-2}$在第一象限为减函数,
∴m2+m-2<0,
解得-2<m<1,
故答案为:(-2,1)
点评 本题主要考查幂函数的性质,根据幂函数的单调性和指数之间的关系是解决本题的关键.

练习册系列答案
相关题目
20.sin(θ+75°)+cos(θ+45°)-$\sqrt{3}$cos(θ+15°)=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
15.某学校有学生2500人,教师350人,后勤职工150人,为了调查对食堂服务的满意度,用分层抽样从中抽取300人,则学生甲被抽到的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{2500}$ | D. | $\frac{1}{3000}$ |
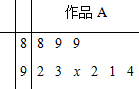 我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.