设x.y满足$\left\{\begin{array}{l}{2x+y≤10}\\{x+2y≤14}\\{x+y≥6}\end{array}\right.$.则xy的最大值为$\frac{25}{2}$．题目和参考答案——青夏教育精英家教网——

题目内容

17．设x，y满足$\left\{\begin{array}{l}{2x+y≤10}\\{x+2y≤14}\\{x+y≥6}\end{array}\right.$，则xy的最大值为$\frac{25}{2}$．

分析作出不等式组对应的平面区域，利用基本不等式进行求解即可．

解答解：作出不等式组对应的平面区域如图：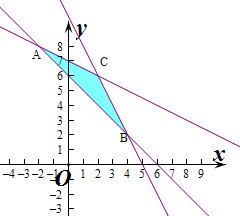
由图象知y≤10-2x，
则xy≤x（10-2x）=2x（5-x））≤2（$\frac{x+5-x}{2}$）²=$\frac{25}{2}$，
当且仅当x=$\frac{5}{2}$，y=5时，取等号，
经检验（$\frac{5}{2}$，5）在可行域内，
故xy的最大值为$\frac{25}{2}$，
故答案为：$\frac{25}{2}$．

点评本题主要考查线性规划以及基本不等式的应用，利用数形结合是解决本题的关键．

练习册系列答案

名师题库系列答案

本土教辅名校学案黄冈期末全程特训卷系列答案

易学练系列答案

名师点拨期末冲刺满分卷系列答案

名校名师培优作业本加核心试卷系列答案

名师点拨培优训练系列答案

期末满分冲刺卷系列答案

达标测试系列答案

全程金卷系列答案

亮点激活精编提优大试卷系列答案

相关题目

7．判断下列语句是不是命题，如果是，说明是全称命题还是特称命题．
（1）任何一个实数除以1，仍等于这个数；
（2）三角函数都是周期函数吗？
（3）有一个实数x，x不能取倒数；
（4）有的三角形内角和不等于180°．

8．已知tanα-tanβ=2tan²αtanβ，α，β≠$\frac{kπ}{2}$（k∈Z），求$\frac{sin（2α+β）}{sinβ}$值．

5．函数f（x）=${x}^{{m}^{2}+m-2}$在第一象限为减函数，则m的取值范围是（-2，1）．

12．曲线y=5sin（2x+$\frac{π}{6}$）与直线y=x共有7个公共点，与曲线y=log₂x共有21个公共点．

2．平面直角坐标系中，O为坐标原点，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，其中$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，1），平面区域D由所有满足$\overrightarrow{OP}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$，（0≤μ≤λ≤1）的点P（x，y）组成，点P使得z=ax+by（a＞0，b＞0）取得最大值3，则$\frac{1}{a}$+$\frac{2}{b}$的最小值是（　　）

9．函数y=lg（x²-2x-3）的定义域是（　　）

{x|x＜-1或x＞3}

{x|x＞-3或x＞1}

6．李老师从课本上抄录一个随机变量ξ的概率分布列如表：

x	1	2	3
P（ξ=x）	！	？	！

请小王同学计算ξ的数学期望．尽管“？”处完全无法看清，且两个“！”处字迹模糊，但能断定这两个“！”处的数值相同．据此，小王给出了Eξ的正确答案为（　　）

7．角-2015°所在的象限为（　　）