题目内容
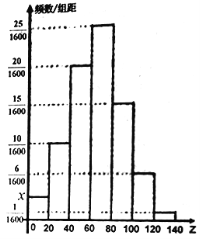
【题目】某校高三学生数学调研测试后,随机地抽取部分学生进行成绩统计,如图所示是抽取出恶报的所有学生的测试成绩统计结果的频率分布直方图。

(1)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计该校高三学生数学调研测试的平均分;
(2)用分层抽样的方法在分数段为![]() 的学生中抽取一个容量为6的样本,则
的学生中抽取一个容量为6的样本,则![]() 的学生分别抽取多少人?
的学生分别抽取多少人?
(3)将(2)中抽取的样本看成一个总体,从中任取2人,求恰好有1人在分数段![]() 的概率。
的概率。
【答案】(1)98(2)2(3)![]()
【解析】
试题分析:(1)同一组数据常用该组区间的中点值作为代表,将中点值与每一组的频率相差再求出它们的和即可求出本次考试的平均分;(2)先计算出在[110,120)、[120,130)分数段抽取的人数比例,再有样本的容量求出抽取的人数;(3)设从样本中任取2人,至多有1人在分数段[120,130)为事件A,然后列出基本事件空间包含的基本事件,以及事件A包含的基本事件,最后将包含事件的个数求出题目比值即可
试题解析:(1)该校高三学生数学调研测试的平均分为
![]() =75×0.005×10+85×0.020×10+95×0.035×10+105×0.025×10+115×0.010×10+125×0.005×10=98(分) 4分
=75×0.005×10+85×0.020×10+95×0.035×10+105×0.025×10+115×0.010×10+125×0.005×10=98(分) 4分
(2)设在(110,120],(120,130]的学生分别抽取x、y人,
根据分层抽样的方法得:x:y=2:1
∵在(110,130]的学生中抽取一个容量为6的样本,
∴在(110,120]分数段抽取4人,在(120,130]分数段抽取2人; 7分
(3)设从样本中任取2人,恰好有1人在分数段(110,120]为事件A,
在(110,120]分数段抽取4人,记为1、2、3、4;在(120,130]分数段抽取2人,分别记为a,b;则基本事件空间包含的基本事件有:(1,2)、(1,3)、(1,4)、(1,a)、(1,b)、(2,3)、(2,4)、(2,a)、(2、b)、(3,4)、(3,a)、(3,b)、(4,a)、(4,b)、(a,b)共15种. 10分
则事件A包含的基本事件有:(1,a)、(1,b)、(2,a)、(2、b)、(3,a)、(3,b)、(4,a)、(4, b)共8种,根据古典概型的计算公式得,P(A)=![]() . 12分
. 12分

 阅读快车系列答案
阅读快车系列答案【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II) 在既参加书法社团又参加演讲社团的8名同学中,有5名男同学![]() ,3名女同学
,3名女同学![]() ,现从这5名男同学和3名女同学中各随机选1人,求
,现从这5名男同学和3名女同学中各随机选1人,求![]() 被选中且
被选中且![]() 未被选中的概率。
未被选中的概率。
【题目】在一次文、理学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩为![]() ,文综成绩为
,文综成绩为![]() ,
,![]() 为
为![]() ,将
,将![]() 值分组统计制成下表:
值分组统计制成下表:
分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) | [120,140] |
频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
并将其中女生的![]() 值分布情况制成频率分布直方图(如图所示).
值分布情况制成频率分布直方图(如图所示).
(1)若已知直方图中[60,80)频数为25,试分别估计全体学生中,![]() 的男、女生人数;
的男、女生人数;
(2)记![]() 的平均数为
的平均数为![]() ,如果
,如果![]() 称为整体具有学科学习倾向,试估计高一年段女生的
称为整体具有学科学习倾向,试估计高一年段女生的![]() 值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.