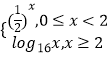题目内容
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
【答案】
(1)解:根据表中的数据,计算观测值得;
k2= ![]() =
= ![]() ≈4.110>3.841,
≈4.110>3.841,
因此在犯错误的概率不超过0.05的前提下,认为视力与学习成绩有关系;
(2)解:依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,
X可取0,1,2,3;
则P(X=0)= ![]() =
= ![]() ,P(X=1)=
,P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,P(X=3)=
,P(X=3)= ![]() =
= ![]() ;
;
所以,X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望为E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =1.
=1.
【解析】(1)根据表中的数据,计算观测值k2 , 对照数表,得出结论;(2)求出X的取值,计算对应的频率,求出X的分布列与数学期望值.

【题目】如图是2012年在某大学自主招生考试的面试中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
7 | 9 | ||||
8 | 4 | 4 | 6 | 4 | 7 |
9 | 3 |
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4