题目内容
10.已知向量$\overrightarrow{a}$=(x+z,3),$\overrightarrow{b}$=(2,y-z),且$\overrightarrow{a}$⊥$\overrightarrow{b}$.若x,y满足不等式$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤2}\end{array}\right.$,则z的取值范围为( )| A. | [-6,4] | B. | [-4,6] | C. | [0,4] | D. | [0,6] |
分析 由$\overrightarrow{a}$⊥$\overrightarrow{b}$,得到z=2x+3y,画出满足条件的平面区域,通过图象读出即可.
解答 解:∵$\overrightarrow{a}$=(x+z,3),$\overrightarrow{b}$=(2,y-z),
又∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴(x+z)×2+3×(y-z)=2x+3y-z=0,
即z=2x+3y,
画出满足条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤2}\end{array}\right.$的平面区域,如图示: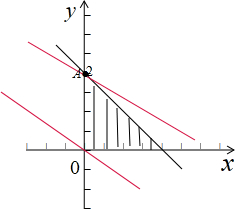 ,
,
由z=2x+3y得:y=-$\frac{2}{3}$x+$\frac{z}{3}$,
显然:直线过原点是z最小是0,直线过A(0,2)时,z最大是6,
故选:D.
点评 本题考查了向量垂直的性质,考查简单的线性规划问题,是一道基础题.

练习册系列答案
相关题目
1.已知函数f(x)及其导数′(x),若存在x0,使得f(x)=f′(x),则称x0是f(x)的一个“巧值点”,下列函数中,有“巧值点”的是( )
①f(x)=x2,
②f(x)=e-x,
③f(x)=lnx,
④f(x)=tanx,
⑤f(x)=x+$\frac{1}{x}$.
①f(x)=x2,
②f(x)=e-x,
③f(x)=lnx,
④f(x)=tanx,
⑤f(x)=x+$\frac{1}{x}$.
| A. | ①③⑤ | B. | ①③④ | C. | ①②③④ | D. | ①②⑤ |
18.设全集U=R,A={x|3x(x-2)>1},B={x|y=lg(1-x)},则图中阴影部分所表示的集合为( )


| A. | {x|x<0} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x<1} |
2.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )


| A. | r2<r4<0<r3<r1 | B. | r4<r2<0<r1<r3 | C. | r4<r2<0<r3<r1 | D. | r2<r4<0<r1<r3 |
19.利用演绎推理的“三段论”可得到结论:函数f(x)=lg$\frac{1-x}{1+x}$的图象关于坐标原点对称,那么,这个三段论的小前提是( )
| A. | f(x)是增函数 | B. | f(x)是减函数 | C. | f(x)是奇函数 | D. | f(x)是偶函数 |