题目内容
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
【答案】①③④
【解析】
试题分析:函数中存在“倍值区间”,则①![]() 在
在![]() 内是单调函数;②
内是单调函数;②![]() ,
,![]() 或
或![]() ,
, ![]() ,①
,①![]() 若存在“倍值区间”
若存在“倍值区间”![]() ,则
,则![]() ,∴
,∴![]() ,若存在“倍值区间”
,若存在“倍值区间”![]() ;②
;②![]() 若存在“倍值区间”
若存在“倍值区间”![]() ,则
,则![]() ,
,![]() ,构建函数
,构建函数![]() ,∴
,∴![]() ,∴函数在
,∴函数在![]() 上单调减,在
上单调减,在![]() 上单调增,∴函数在
上单调增,∴函数在![]() 处取得极小值,且为最小值.∵
处取得极小值,且为最小值.∵![]() ,∴
,∴![]() ,∴
,∴![]() 无解,故函数不存在“倍值区间”;③
无解,故函数不存在“倍值区间”;③![]() 若存在“倍值区间”
若存在“倍值区间”![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,
,![]() ,若存在“倍值区间”
,若存在“倍值区间”![]() ;④
;④![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ).不妨设
).不妨设![]() ,则函数在定义域内为单调增函数,若存在“倍值区间”
,则函数在定义域内为单调增函数,若存在“倍值区间”![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() 是方程
是方程![]() 的两个根,∴
的两个根,∴![]() 是方程
是方程![]() 的两个根,由于该方程有两个不等的正根,故存在“倍值区间”
的两个根,由于该方程有两个不等的正根,故存在“倍值区间”![]() ;综上知,所给函数中存在“倍值区间”的有①③④.
;综上知,所给函数中存在“倍值区间”的有①③④.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】第![]() 届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取![]() 名进行了问卷调查,得到
名进行了问卷调查,得到![]() 列联表,从这
列联表,从这![]() 名同学中随机抽取
名同学中随机抽取![]() 人,抽到“收看奥运会足球赛 ”的学生的概率是
人,抽到“收看奥运会足球赛 ”的学生的概率是![]() .
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
(1)请将上面的![]() 列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
(2)若从这![]() 名同学中的男同学中随机抽取
名同学中的男同学中随机抽取![]() 人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为
人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
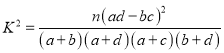 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|